PDEs

Research Projects

The Navier-Stokes equation. In the upcoming work [1], we prove existence of 2D periodic orbits in the forced Navier-Stokes (NS) equation. We consider low Reynolds number and a time independent forcing term leading to Taylor-Green flows. We apply the rotational and solve for the periodic orbits in the vorticity equation. Using a bifurcation analysis and a continuation method, we prove existence of some periodic orbits in a non perturbative regime. Using the symmetry of the orbits, we formulate a zero finding problem in a Banach algebra of geometrically decaying space-time symmetric Fourier coefficients and we apply a Newton-Kantorovich argument to obtain the computer-assisted proofs. Since the forcing term is time independent, we can recover rigorously the periodic orbits for the original divergent free velocity NS equation.

The ill-posed Boussinesq equation. Besides the recent successes of the application of rigorous numerics in dynamics in the last 30 years, ill-posed equations and strongly indefinite problems have not received much attention, which is perhaps not surprising as they do not naturally lead to the notion of a dynamical system. In [2], we proved existence of many periodic orbits in the ill-posed Boussinesq equation. The Boussinesq equation has been investigated extensively because of its role in the theory of shallow water waves. Since the equation is a Hamiltonian PDE, we use symmetries to isolate the solutions in order to apply the contraction mapping theorem to prove their existence.

The Kuramoto-Sivashinsky equation. This model is a fourth-order dissipative PDE with a viscosity damping parameter and is a popular model to analyze weak turbulence or spatiotemporal chaos. In the paper [3], we introduced a general framework for the numerical computation and a posteriori verification of invariant objects of evolution equations. We apply this general theory in [4], where we compute rigorously a global continuous branch of periodic orbits in the Kuramoto-Sivashinsky equation. We solve an eigenvalue problem and then compute stable and unstable bundles attached to the orbits. Using that information we conclude about linear instability of the periodic orbits.

Co-existence of hexagons and rolls. In the paper [1], we solve a conjecture raised in [A. Doelman et al., European J. Appl. Math. 14 (2003), no. 1, 85-110] about the existence of fronts with vanishing wave speed that correspond to spatially co-existing patterns. More precisely, we prove existence of spatial connections of stripe and hexagon patterns in the supercritical cubic Swift-Hohenberg equation with a term that breaks the up-down symmetry. The problem is cast as a spatial boundary value problem with boundary conditions in the unstable/stable manifolds of the asymptotic states. With suitable parametrization of these local invariant manifolds, the connection problem is solved by a rigorous computational method via Chebyshev series.

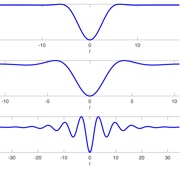
Traveling waves in the suspension bridge equation. We consider the suspension bridge equation with an exponential nonlinearity, where the solution describes the deflection of the roadway from the rest state as a function of time and the spatial variable (in the direction of traffic). Paper [2] is concerned with proving the existence of traveling wave solutions describing a disturbance propagating at velocity c along the surface of the bridge. In particular, we apply a computer-assisted proof method to show that there is a large range of velocities for which such a solitary wave exists for a continuous range of parameter values. This partially solves a conjecture raised by Y. Chen and P. J. McKenna [Philos. Trans. Roy. Soc. London Ser. A 355 (1997), no. 1732, 2175-2184].

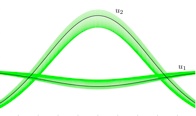
Existence of pulses in the Gray-Scott PDE model. In [3] we propose a rigorous numerical technique for the computation of symmetric connecting orbits for ordinary differential equations. The idea is to solve a projected boundary value problem (BVP) in a function space via a fixed point argument. The formulation of the projected BVP involves a high order parameterization of the invariant manifolds at the steady states. Using this parameterization, one can obtain explicit exponential asymptotic bounds for the coefficients of the expansion of the manifolds. Combining these bounds with piecewise linear approximations, one can construct a contraction in a function space whose unique fixed point corresponds to the wanted connecting orbit. We have implemented the method to demonstrate its effectiveness, and we have used it to prove the existence of a family of even homoclinic orbits for the Gray-Scott equation.

[1] J.B. van den Berg, A. Deschênes, J.-P. Lessard and J.D. Mireles James. Stationary coexistence of hexagons and rolls via rigorous computations. SIAM Journal on Applied Dynamical Systems, 14(2): 942-979, 2015. (pdf).

[2] J.B. van den Berg, M. Breden, J.-P. Lessard and M. Murray. Continuation of homoclinic orbits in the suspension bridge equation: a computer-assisted proof, To appear in Journal of Differential Equations. (pdf)

[3] J.B. van den Berg, J.-P. Lessard, J.D. Mireles James and K. Mischaikow. Rigorous numerics for symmetric connecting orbits: even homoclinics of the Gray-Scott equation. SIAM Journal on Mathematical Analysis, 43 (4): 1557–1594, 2011. (pdf)

[1] J.B. van den Berg, M. Breden, J.-P. Lessard and L. van Veen. Space-time periodic solutions of the Taylor-Green flow in the Navier-Stokes equations, 2017. In preparation.

[2] R. Castelli, M. Gameiro and J.-P. Lessard. Rigorous numerics for ill-posed PDEs: periodic orbits in the Boussinesq equation. To appear in Archive for Rational Mechanics and Analysis. (pdf)

[3] J.-L. Figueras, M. Gameiro, J.-P. Lessard and R. de la Llave. A framework for the numerical computation and a posteriori verification of invariant objects of evolution equations. SIAM Journal on Applied Dynamical Systems, 16(2): 1070-1088, 2017. (pdf)

[4] M. Gameiro and J.-P. Lessard. A posteriori verification of invariant objects of evolution equations: periodic orbits in the Kuramoto-Sivashinsky PDE. SIAM Journal on Applied Dynamical Systems, 16(1): 687-728, 2017. (pdf)

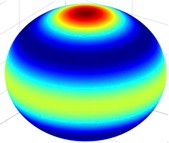
Radially symmetric solutions. In [6], we introduce a computer-assisted approach based on Taylor series to prove existence of radially symmetric solutions of a nonlinear Laplace-Beltrami operator on the sphere and radially symmetric equilibria of the Swift-Hohenberg equation on the 3D unit ball. The proofs are obtained by solving for the coefficients of the Taylor series of the solutions in a Banach space of geometrically decaying sequences. The tool that allows us to advance from numerical simulation to mathematical proof is the Banach contraction theorem.

Steady states of PDEs. The first step in understanding the dynamics of a parabolic PDE is to identify the set of equilibria. This is particularly true for gradient PDEs, where the global attractor consists of steady states and connecting orbits between them. In the papers [1,2], we introduce a general rigorous computational method to prove existence of equilibria in one-dimensional PDEs, and we generalize the method for higher-dimensional PDEs in [3,4,5]. We introduce general analytic estimates (convolution estimates) in the class of sequences with algebraic decay. We apply the method to prove existence of steady states in the 3D Cahn-Hilliard equation and the 3D Swift-Hohenberg equation on rectangular domains.

[1] S. Day, J.-P. Lessard and K. Mischaikow. Validated continuation for equilibria of PDEs. SIAM Journal on Numerical Analysis, 45 (4): 1398–1424, 2007. (pdf)

[2] M. Gameiro, J.-P. Lessard and K. Mischaikow. Validated continuation over large parameter ranges for equilibria of PDEs. Mathematics and computers in simulation, 79 (4): 1368–1382, 2008. (pdf)

[3] M. Gameiro and J.-P. Lessard. Analytic estimates and rigorous continuation for equilibria of higher-dimensional PDEs. Journal of Differential Equations, 249 (9): 2237–2268, 2010. (pdf)

[4] M. Gameiro and J.-P. Lessard. Rigorous computation of smooth branches of equilibria for the three-dimensional Cahn-Hilliard equation. Numerische Mathematik, 117 (4): 753–778, 2011. (pdf)

[5] M. Gameiro and J.-P. Lessard. Efficient rigorous numerics for higher-dimensional PDEs via one-dimensional estimates. SIAM Journal on Numerical Analysis, 51(4): 2063-2087, 2013. (pdf)

[6] I. Balazs, J.B. van den Berg, J. Courtois, J. Dudas, J.-P. Lessard, A. Vörös- Kiss, JF Williams and X.Y. Yin. Computer-assisted proofs for radially symmetric solutions of PDEs, 2017. (pdf)

[7] J.-P. Lessard and J.D. Mireles James. Computer assisted Fourier analysis in sequence spaces of varying regularity. SIAM Journal on Mathematical Analysis, 49(1), 530–561, 2017. (pdf)

[8] J.-P. Lessard, E. Sander and T. Wanner. Rigorous continuation of bifurcation points in the diblock copolymer equation, To appear in Journal of Computational Dynamics. (pdf)

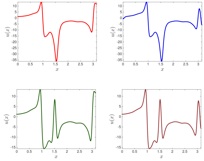
Breakdown of analyticity. In [7], we explore the breakdown of analyticity of steady states in the spatially inhomogeneous Fisher PDE with a kernel function. An abstract a-posteriori theorem is employed in order to obtain existence and regularity results for C^k or analytic kernels. The main tools are certain infinite sequence spaces of rapidly decaying coefficients: we employ sequence spaces of algebraic and exponential decay rates in order to characterize the regularity of our results. We examine the effectiveness of spaces of algebraic decays for studying solutions of problems near the breakdown of analyticity in Fisher’s equation.

Saddle-node and pitchfork bifurcations in PDEs. In [8], we develop a method to compute rigorously curves of saddle-node and pitchfork bifurcations of equilibria of PDEs. For saddle-node, this is accomplished by considering an extended system which encodes both the existence condition for the equilibrium point and the existence of a one-dimensional non-degenerate kernel of the linearization. In case of symmetry breaking pitchfork bifurcations, we employ the method introduced in [Werner & Spence, SIAM J. Numer. Anal. 21 (1984), no. 2, 388-399] to derive a well-defined continuation problem. We apply the method to compute rigorously global branches of saddle-node and pitchfork bifurcation points in the one-dimensional diblock-copolymer PDE model.

Dynamics of Parabolic Partial Differential Equations (PDEs)

A main part of my research focuses on developing a functional analytic approach to study the dynamics of parabolic PDEs. Combining the strength of numerical analysis, topological methods, nonlinear analysis, scientific computing, continuation methods, functional analysis and fixed point theory, one of my goal is to develop a general computational theory to obtain computer-assisted proofs of existence of special types of dynamical objects in infinite dimensional dynamical systems arising from studying PDEs, that is steady states, periodic orbits, traveling waves, invariant manifolds, connecting orbits, bifurcations, etc.

Periodic Orbits in Dissipative PDEs

Traveling and Standing Waves in PDEs

Equilibrium Solutions in PDEs