Research visualizations

This page displays some images of the geometric spaces that I study. The three-dimensional renderings were created using surfex.

The Stokes groupoids

The Stokes groupoids are Lie groupoids that serve as the universal domains of definition for the parallel transport of meromorphic connections on Riemann surfaces. Many of these groupoids have simple descriptions in terms of classical geometry. Below are some examples; clicking on the images will open a new tab or window with an interactive Java applet that demonstrates the groupoid structure. These applets were created using GeoGebra.

A pair groupoid	A twisted pair groupoid

Poisson modules and degeneracy loci

Here is a poster poster in PDF format that gives a summary of my paper with Marco Gualtieri, entitled "Poisson modules and degneracy loci":

The poster was presented at the Poisson 2012 conference, and includes some 3D pictures of one of Feigin and Odesskii's elliptic Poisson structures on P⁴.

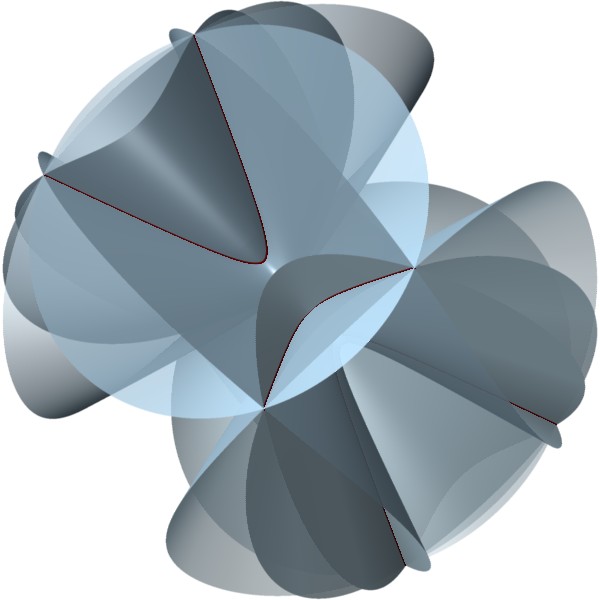
Poisson structures on P³

The variety parametrizing Poisson structures on projective three space has six irreducible components. Here are some pictures of the symplectic leaves and zero loci of Poisson structures from the various components (click to enlarge). See also Chapter 8 in my thesis.

L(1,1,1,1)	R(2,2)	S(2,3)
L(1,1,2)	R(1,3)	E(3)