Undergraduate Student Research Projects
I take on summer students, through the NSERC Undergraduate Student Research Awards (USRA) programme (Canadian residents only), and also through the new McGill SURA awards (international students also elligible). See the
websites for details. As of Fall 2016 the relevant pages are Mathematics Dept Info, McGill Science NSERC Info, McGill GPS NSERC Info, McGill Science SURA Info and NSERC USRA, BUT beware that some of these may move or change for future years.Usually I'd expect you to be a Math Honours or Majors student, reasonably advanced in your degree, with some analysis courses and a Numerical Analysis course in your resume, and a cumulative GPA above 3.50.
The deadline for applications is usually in late January. If interested contact me early January, or better still before Christmas. But I am interested in applications right up to the deadline. Most of my current research revolves around analysis and numerical analysis of delay and advance-delay equations, and recent projects have explored aspects of that. If anything below interests you, contact me.
Available Projects
Analysis and/or Numerics for Delay and Advance-Delay Differential Equations
My current research interests centre around dynamical systems and numerical analysis, particularly in the area of delay differential equations and advance-delay differential equations. A very simple example of a delay equation isu'(t)=-γu(t)-κu(t-a)
Where γ>0 and a>0 and κ≥0 are constants. If κ=0 this is a very trivial ordinary differential equation. But for κ>0 and a>0 it is a delay differential equation (DDE) with delay a, and becomes very interesting. If you haven't seen an equation like this before, think about it for a while. If you assume that u(t)=ceλt is a solution, you ought to be able to find an equation that λ satisfies (which doesnt involve t). A harder exercise is to show that this equation has infinitely many complex solutions. Now since the original equation was linear, any linear combination of solutions is a solution and so the solution space is infinite dimensional. The stability of the trivial solution u(t)=0 is also interesting; it loses stability as κ increases.
Adding nonlinear terms makes the equation much more interesting, now bifurcations can occur. Adding extra delays or non-constant delays add extra complications, especially if the delays are state-dependent, that is the delay depends on the state of the system. The following model DDE problem with two state-dependent delays has been the subject of much recent research.
Here the value of u'(t) depends on the values of u at times t, t- a1 - c1 u(t), and t- a2 - c2 u(t). This DDE is nonlinear and it is not possible to construct solutions with explicit forms. However, the only nonlinearities arise through the state-dependency; if we set c1=c2=0 to remove the state-dependency then the equation also becomes linear. This means that any interesting dynamics displayed by this model state-dependent DDE are driven by the state-dependency, and it is a good model for studying the possible dynamics that state-dependency of delays can entail. Those dynamics have been found to include co-existing stable periodic orbits, period-doublings and stable invariant tori and torus break up.
I don't expect prior knowledge of delay differential equations (they are not taught in undergraduate courses), and so a significant component of the project would be learning about these fascinating and complicated differential equations. Additional facets of the project could be analytical, computational or applications based depending on your interests and expertise.
I have several computational projects suitable for undergraduate summer research, which would involve numerically exploring the dynamics and bifurcation structures of a particular DDE. Such a project would involve learning and using DDEBiftool, a suite of matlab routines for studying bifurcations in delay differential equations. Previous experience with DDEBiftool is not necessary, but a strong background in computing is. Several previous students (see Gonzalez, Homouyanfar, DeMasi and Upham below) have completed computational projects very successfully.
Theoretical DDE projects are hard to devise; state-dependent DDEs can be formulated as nonlinear infinite dimensional dynamical systems on functions spaces, and existing theory is nontrivial to say the least. Nevertheless, several students have made significant progress in constructing the form of some of the possible periodic solutions of the model problem above in the singular limit as ε→0 (see Bernucci, Snarski and Zhang below).
The main application of DDEs that I am currently working on is the human hematological system, which can be modelled by a system of delay and integral differential equations. Mike Mackey and his group have spent many years developing this model, and using it to explain dynamical diseases. Many undergraduate students have contributed to the development of the model. Our current focus is on the modelling and treatment of chemotherapy induced neutropenia, and this would be an excellent project for a student with an interest in mathematical physiology to be involved in.
If some of this sounds potentially interesting and challenging, contact me.
Previous Projects
Previous projects are listed below. I take one or two students most years. These have been funded by- NSERC USRAs (Michael Snarski, Daniel Bernucci, Finn Upham, Myriam Berube),
- McGill SURAs (Dongliang Zhang, Emily Wall, Orianna DeMasi)
- A CAMBAM Undergraduate Research Fellowship (Namdar Homayounfar),
- ISM Undergraduate Summer Scholarships - supervised jointly with my postdoc ( Nicolas Gonzalez, Namdar Homayounfar).
Winter 2015: Mackenzie Pearson (Honours Research Project)
Numerical Methods for Distributed Delay Differential Equations
Distributed delay differential equations are a class of fundamental differential equations whose solutions can be approximated numerically using functional Runge-Kutta methods. However, to evaluate the Runge-Kutta steps an integrand needs to be evaluated. In this project we study the case where this integral is over a semi-infinite interval with integrand decaying appropriately to ensure the functional is bounded. The student will investigate suitable numerical quadrature techniques of the type arising in distributed delay differential equations with unbounded delays and write a report on his findings and give an oral presentation.Summer 2014: Sean Sinclair (SURA Award)
Numerical Methods for State-Dependent Distributed Delay Differential Equations
Many processes are modelled by differential equations subject to delays (DDEs). The numerical analysis and solution of such equations is well developed in the case of discrete delays. However, in some important applications including threshold maturation models in biology, distributed delays arise. In such equations the definition of the differential equation itself involves an integral of the solution over the past. This integration interval may be finite or unbounded, and its length can even be state dependent. The matlab DDE solver, ddesd, only solves DDEs with discrete delays. There is no simple general purpose matlab DDE solver for problems with distributed delays. In this project the student will the basic theory of delay differential equations and their numerical analysis, and develop simple first and second order matlab solvers for a class of distributed delay differential equations. These methods will be tested on distributed DDE models arising from threshold dynamics, including equations arising from the supervisors work with Mike Mackey's group on the human hematological system.Sean's work contributed to
- G. Provencher Langlois, M. Craig, A.R. Humphries, M.C. Mackey, J.M. Mahaffy, J. Bélair, T. Moulin, S.R. Sinclair and L. Wang. Normal and pathological dynamics of platelets in humans, 2016. arXiv:1608.02806 [q-bio.TO]
Summer 2012: Dongliang Zhang (SURA Award)
Periodic Orbits of a Singularly Perturbed State Dependent DDE with independent delays
Many processes are modelled by differential equations subject to delays. In most models and mathematical theory this time delay is fixed, but in application areas there is much evidence of state dependent delays. However, the state dependency is usually suppressed when deriving mathematical models of these processes, because there is little mathematical theory of such equations. We will study a model multiple delay nonlinear differential equation, with independent linearly state-dependent delays which undergoes Hopf bifurcations. Of particular interest are the periodic orbits created in the bifurcations. In previous summer projects geometric techniques for the single delay problem were generalised to the multiple delay problem with dependent delays, and hence some families of periodic orbits were identified for the two delay problem in a singularly perturbed limit. The current project will build on the previous work to find similar families of periodic orbits in the case of two linearly independent delays. The student will learn the basic theory of delay differential equations, and geometric-algebraic techniques used to study the singularly perturbed problem in the single and multiple delay case. He will then use these techniques to construct candidate periodic solutions and will investigate the parameter ranges of their validity, and possible associated bifurcation structures.Summer 2012: Nicolas Gonzalez (ISM Undergraduate Summer Scholarship)
Numerical study of a class of differential equations with two linearly dependent state-dependent delays
Jointly supervised with Renato CallejaWe study a state dependent delay equation with two linear state dependent delays:
For certain values of the parameter this equation undergoes a Hopf bifurcation creating periodic orbits that are of particular interest. Previous projects considered the case when c1 = c2. This assumption makes the delays dependent since the difference between the two dependent delays is equal to the constant a2 - a1, although the delays themselves are not constant.
We consider the more general problem with firstly in the nonsingular case (ε=O(1)) and then in the singular singular limit as ε→0. In this case the delays are independent and new solutions will arise. This problem has yet to be studied systematically. There are some suspected stable periodic solutions found by simulation of the equations, but no study has yet been made of the possible bifurcation diagrams that can arise.
The student will learn basic theory of delay differential equations and learn how to implement code using the numerical integrator DDESD and the numerical continuation software DDEBIFTOOL to approximate and continue numerically periodic solutions to state dependent delay equations. He will review the results obtained on the previous years and perform the corresponding modifications to the software in order to explore the case of independent delays. Initially he will consider the of nonsingular case (ε=1), but if time permits it would also be very interesting to explore how the dynamics change in the limit as ε→0 .
Summer 2012: Namdar Homayounfar (CAMBAM Undergraduate Research Fellowship)
The effect of timing of GCSF administration in neutrophil dynamics
Jointly supervised with Mike Mackey (Physiology), Jacques Belair (Univ de Montréal)This project is an outgrowth of observations in a paper on the effects of combined chemotherapy and granulocyte colony stimulating factor (G-CSF) treatment in a model for the regulation of neutrophil production (Brooks et al., “Neutrophil dynamics after chemotherapy and G-CSF: The role of pharmacokinetics in shaping the response”, J. Theor. Biol. Submitted 2012). Namely in that paper it was observed from numerical simulations that the effect of G-CSF was highly dependent on the timing of administration during the cycles of periodic application of chemotherapy. The nature of this dependence was such that with some timings G-CSF was predicted to have a highly beneficial effect on neutrophil recovery, while with others the effect was actually worse than not administering G-CSF at all.
The student will use a highly simplified version of this model to investigate the origin and nature of these findings, and it is hoped that his results will offer considerable insight into how to better time the administration of G-CSF following chemotherapy. The model will consist of a nonlinear differential delay equation in a parameter range where the single steady state is unstable and there is a stable limit cycle (to mimic the effects of periodic application of chemotherapy). The model will then be investigated for the effects of periodic perturbation by G-CSF, where it is expected that those effects will be significantly dependent on both the phase and amplitude of the G-CSF administration.
Summer 2011: Michael Snarski (NSERC USRA)
Periodic Orbits of a Singularly Perturbed Two State Dependent Delay Differential Equation
Many processes are modelled by differential equations subject to delays. In most models and mathematical theory this time delay is fixed, but in application areas there is much evidence of state dependent delays. However, the state dependency is usually suppressed when deriving mathematical models of these processes, because there is little mathematical theory of such equations. In this project we will study a model multiple delay nonlinear differential equation, with linearly state-dependent delays which undergoes Hopf bifurcations. Of particular interest are the periodic orbits created in the Hopf bifurcations. Last year we extended simple geometric techniques for the single delay problem to the multiple delay problem and hence identified some families of periodic orbits for the two delay problem in a singularly perturbed limit. The current project will build on the previous work to find additional families of periodic orbits, in particular studying the orbits created in a period doubling bifurcation identified in the previous project, and other possible bifurcations in the system.Michael's project was published as part of
- Periodic Solutions of a Singularly Perturbed Delay Differential Equation With Two State-Dependent Delays, A.R. Humphries, D.A. Bernucci, R. Calleja, N. Homayounfar and M. Snarski. Journal of Dynamics and Differential Equations, 28 (2016) 1215-1263.
Summer 2011: Namdar Homayounfar (ISM Undergraduate Summer Scholarship)
Numerical Study Of A Family Of A State Dependent Delay Differential Equations Close To A Singular Limit
Jointly supervised with Renato CallejaNumerical study using ddebiftool to find Hopf bifurcations and the resulting branches of periodic solutions in a family of state dependent delay differential equations close to a singularly perturbed limit. Secondary fold and period doubling bifurcations and the resulting solution branches are also studied. Bifurcations and transitions between unimodal, bimodal, trimodal and quadrimodal periodic solutions are also identified.
Namdar's project was published as part of
- Periodic Solutions of a Singularly Perturbed Delay Differential Equation With Two State-Dependent Delays, A.R. Humphries, D.A. Bernucci, R. Calleja, N. Homayounfar and M. Snarski. Journal of Dynamics and Differential Equations, 28 (2016) 1215-1263.
Summer 2011: Emily Wall (SURA Award)
Phase dynamics of coupled ecological systems
|
Jointly supervised with Fred Guichard (Biology)
This project investigates the effect of weak dispersal coupling with time delay in synchronizing oscillating populations in two identical predator prey patches. The time delay represents the finite transmission time of individuals dispersing, a relevant consideration in spatially separated systems that incorporates characteristics of individual movement through space during dispersal. Reducing the system to a phase model using weakly connected network theory, we find that the time delay can greatly vary the types of stable phase locked states available, as well as enhance or slow the speed of convergence to these states. This adds to our understanding of when weak dispersal can be the cause of synchronization dynamics. |

|
Emily's project was published as
- Synchronization in ecological systems by weak dispersal coupling with time delay, E. Wall, F. Guichard and A.R. Humphries, Theoretical Ecology, (2013). doi:10.1007/s12080-013-0176-6
Summer 2011/Fall 2012: Gabriel Provencher Langlois (Honours Research Project)
Dynamic hematological response to Thrombopoietin
Cyclical Thrombocytopenia (CT) is a hematopoietic disease in which circulating platelet numbers oscillate from normal to virtually zero with periods ranging from 30 to 70 days. Previous mathematical modeling work (Apostu and Mackey, Journal of Theoretical Biol. 2008) has pinpointed likely parameter alterations that lead to a Hopf bifurcation in the platelet control system. One of the outstanding clinical problems is how to effectively treat CT using recombinant thrombopoietin (TPO), which is thought to interfere with apoptosis in platelet precursors in the bone marrow. However, recent clinical attempts by a group in Ontario have had mixed success, and they have approached Prof. Mackey to try to offer a more intelligent pattern of temporal administration of TPO to more effectively regulate platelet levels in the normal range for CT patients. This is to be accomplished through a combination of analytic work augmented by numerical simulations based on the complete mathematical model for human hematopoiesis of Coljin and Mackey (JTB, 2005)Gabriel's project led to
- G. Provencher Langlois, M. Craig, A.R. Humphries, M.C. Mackey, J.M. Mahaffy, J. Bélair, T. Moulin, S.R. Sinclair and L. Wang. Normal and pathological dynamics of platelets in humans, 2016. arXiv:1608.02806 [q-bio.TO]
Summer 2010: Daniel Bernucci (NSERC USRA)
Singularly Perturbed Multiple State Dependent Delay Differential Equations
Many processes are modelled by differential equations subject to delays, where the delays can arise in a number of contexts such as maturation time in population models. In most models and mathematical theory this delay time is fixed, but in application areas there is much evidence of state dependent delays. For example, when the body has deficit of white blood cells, production of new ones is ramped up and they are actually matured faster. However, the state dependency is usually suppressed when deriving mathematical models of these processes, because there is little mathematical theory of such equations. In this project we will study a model multiple delay nonlinear differential equation, with linearly state-dependent delays which undergoes Hopf bifurcations.In this project the student will learn the basic theory of delay differential equations, and some of the numerical methods used to study them (applying existing matlab packages), and apply this knowledge to a study of singularly perturbed state-dependent equations of the form mentioned above. Of particular interest are periodic orbits which exist in and close to a singularly perturbed limit, which have been observed to exist numerically. In the case of a single delay, simple geometry determines the form of the orbit. The student will use a generalisation of these simple techniques to study the possible periodic orbits in the singular limit for two state-dependent delays, and how they depend on the parameters in the system, and will also undertake a numerical investigation of these orbits.
Daniel's project was published as part of
- Periodic Solutions of a Singularly Perturbed Delay Differential Equation With Two State-Dependent Delays, A.R. Humphries, D.A. Bernucci, R. Calleja, N. Homayounfar and M. Snarski. Journal of Dynamics and Differential Equations, 28 (2016) 1215-1263.
Summer 2009: Orianna DeMasi (SURA Award)
Analysis and Numerical Analysis of State Dependent Delay Differential Equations
|
Many processes are modelled by differential equations subject to delays, where the delays can arise in a number of
contexts such as maturation time in population models. In most models and mathematical theory this delay time is
fixed, but in application areas there is much evidence of state dependent delays. For example, when the body has
deficit of white blood cells, production of new ones is ramped up and they are actually matured faster. However, the
state dependency is usually suppressed when deriving mathematical models of these processes, because there is
little mathematical theory of such equations. In this project we will study a model multiple delay nonlinear delay
differential equation, with linearly state-dependent delays which can undergo Hopf bifurcations, and also has
inaccessible regions of phase space (where the equations become advance-delayed and are no longer well posed
as initial value problems).
In this project the student will learn the basic theory of delay differential equations, and some of the numerical methods used to study them (applying existing matlab packages), and apply this knowledge to a study of state-dependent equations of the form mentioned above. Of particular interest are the Hopf bifurcations, the evolution of the periodic orbits created in the bifurcations as parameters are varied, and the possibility of multiple co-existing periodic orbits, or even multiple Hopf bifurcations. The overall aim is to increase the understanding of model state-dependent problems, so that in future more applicable equations can be tackled. |
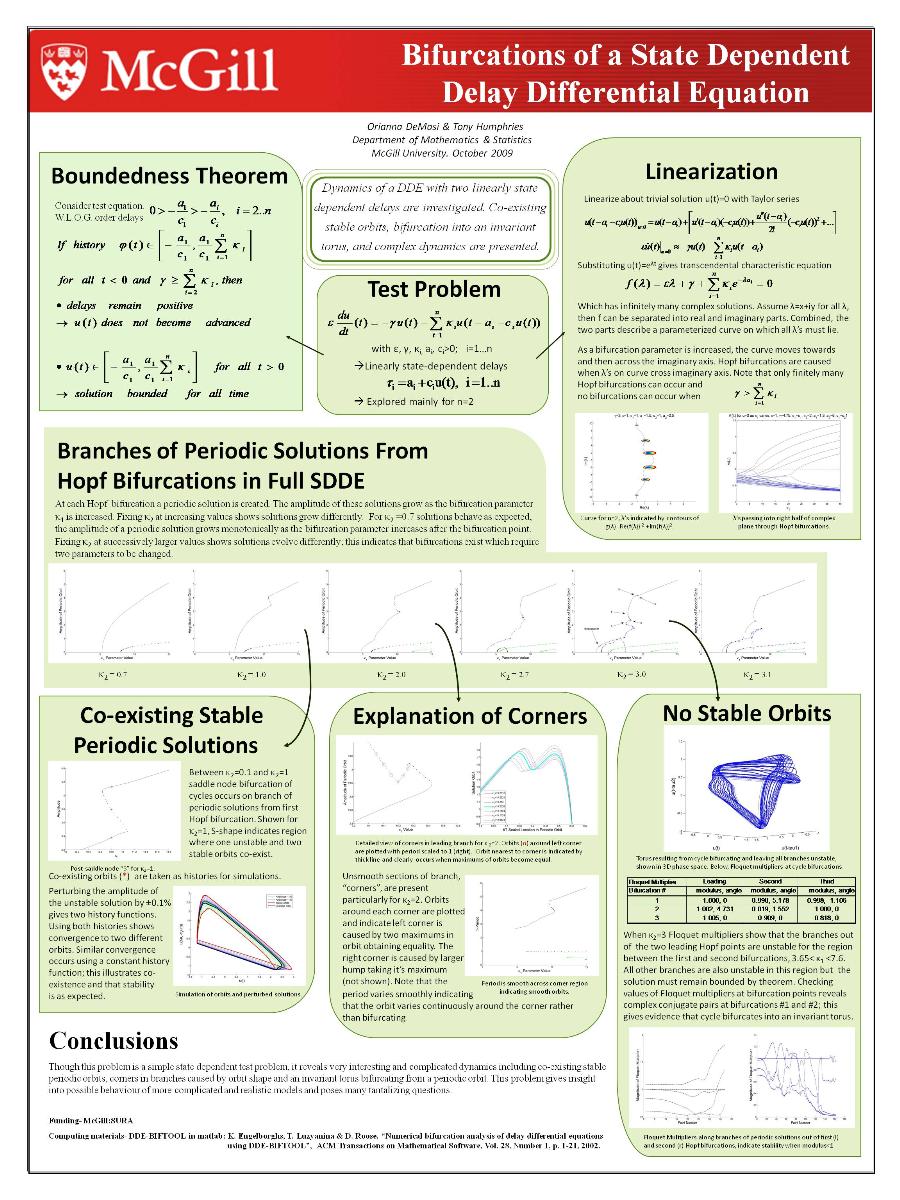
|
Orianna's did all of the above and more, finding stable invariant tori in the flow, as well as the co-existing stable periodic orbits. Her work formed the core of
- Dynamics of a Delay Differential Equation With Multiple State Dependent Delays, A.R. Humphries, O.A. DeMasi, F.M.G. Magpantay and F. Upham. Disc. Cont. Dynam. Syst. series A, 32 (2012) 2701 - 2727.
Summer 2008: Finn Upham (NSERC USRA)
Model Problems in State Dependent Delay Equations
Many processes are modelled by differential equations subject to delays, where the delays can arise in a number of contexts such as maturation time in population models, or communication time between spatially located components of a system. In most models and mathematical theory this delay time is fixed, but in application areas there is much evidence of state dependent delays. For example, when the body has deficit of white blood cells, production of new ones is ramped up and they are actually matured faster. However, the state dependency is usually suppressed when deriving mathematical models of these processes, because there is little mathematical theory of such equations. There is a model problem due to Mallet-Paret and co-workers where the delay is linearly state dependent, which leads to a region of phase space which is inaccessible, because the delay term becomes advanced there. Multiple delay versions of this problem, are in general illposed as retarded equations because solutions may enter the inaccessible region. In this project the student will learn the basic theory of delay differential equations and study model state dependent delay equations, such as the one mentioned, and seek to identify parameter regions for which the initial value problem is well posed as a retarded delay equation. She will also conduct some numerical studies (applying existing matlab packages) on the behaviour of solutions in the case of retarded equations, and finally investigate the possibility of bounded solutions in parameter regimes where the state-dependent arguments become advanced.Finn's work was published as part of
- Dynamics of a Delay Differential Equation With Multiple State Dependent Delays, A.R. Humphries, O.A. DeMasi, F.M.G. Magpantay and F. Upham. Disc. Cont. Dynam. Syst. series A, 32 (2012) 2701 - 2727.
Summer 2004: Myriam Berube (NSERC USRA)
Travelling Waves and Differential Equations with Advances and Retards
Functional Differential Equations (FDEs) with advances and retards such as the discrete Fitzhugh-Nagumo (dFN) equation
-cu'(t)=u(t+1)-2u(t)+u(t-1)-f(u(t))-v(t)
-cv'(t)=b(u(t)-rv(t))
arise naturally as boundary value problems when seeking travelling waves or pulses for lattice differential equations, and in other applications. Whilst equations where the velocity depends on both the past and future positions may seem crazy when you first see them, they are incredibly fascinating really. The dFN equations are used to model nerve impulses in mylineated nerve fibres, and understanding their behaviour is an important first step before modelling demylineation, a factor in MS. Solving the equations analytically is usually impossible except for piecewise linear nonlinearities.
In this project the student will learn about travelling waves and FDEs and numerically compute travelling pulse solutions to the dFN equations with the naturally arising cubic nonlinearity. These solutions will be found by homotopying from known solutions in the idealised piecewise linear case, using the supervisors previously developed collocation code for solution and parameter continuation of FDE boundary value problems. This is an exciting project; Elmer & Van Vleck have only recently found the pulse solutions in the piecewise linear dFN, and the cubic case has not previously been studied in detail.