Applied Mathematics
Introduction
The language, tools and theorems of mathematics are applied in a vast range of disciplines within
engineering and computer science, the physical sciences, the
biomedical sciences, management and economics, psychology, etc. As a field of study and
research applied mathematics lies at the borderline between mathematics and
its applications. While not easily defined with any great precision applied mathematics
involves the application of interesting mathematical tools to significant applied
problems or to the development of novel mathematics adapted to particular applications.
Applied mathematicians use mathematical models to better understand ,and
possibly solve, real-life problems.
Research Areas in Applied Mathematics

-
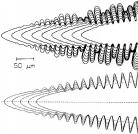
Crystal Growth (Jian-Jun
Xu): On the right you see a snow flake. When nature generates such
a snow flake, it is solving a moving boundary value problem. Next to it
you can see on top experimental data of a growing branch of a snow flake
and below the solution of the governing equations obtained by asymptotic
analysis. Click on the images to see a blowup.
-
Mathematical Physics (Charles
Roth): Theoretical Atomic, Nuclear and Molecular Spectroscopy.
-
Physiology and Nonlinear Dynamics
(Leon Glass
M. Mackey)
-
Computational Fluid Dynamics
(Sherwin Maslowe,
Jian-Jun Xu,
Peter Bartello):
The sequence of images below shows the simulation of a rising atmospheric
thermal. The colours show the potential temperature variation from
blue to red, representing cold to warm fluid. The simulation was
initialised (left panel) with a warm layer of fluid near the
relatively cooler surface. Buoyancy induces the upwards motion depicted
in the other three panels.

 Computational Electromagnetics
(Nilima Nigam): The image shows a finite element
simulation of a cavity problem. If you click on the image, the triangular mesh is clearly visible;
the quantity plotted is the electric potential for a cavity with an inclusion of different
electrical properties.
Computational Electromagnetics
(Nilima Nigam): The image shows a finite element
simulation of a cavity problem. If you click on the image, the triangular mesh is clearly visible;
the quantity plotted is the electric potential for a cavity with an inclusion of different
electrical properties.
- Computational Biology (David Bryant, Nilima Nigam): Computational mathematical sciences are
now having a huge impact on the biological sciences, from models of disease-spread to gene
transcription to evolutionary biology.
- Computational Statistical Mechanics (Paul Tupper)
Practical and theoretical issues in the simulation of complex systems.
Methods for multiscale simulation in materials science.
- Biomolecular networks:
(Peter Swain): The
ability to
process and act on information is fundamental to
life. Complex biochemical networks in all living cells transduce
signals from the outside world to the genome. Through modelling and
collaborative experiment, my research is aimed at uncovering the
`design' of these networks, to explore why one network architecture
has been adopted by evolution over another, and ultimately to
understand how cells `think'.

- Control Theory for Partial Differential Equations (Georg
Schmidt): Controlling the behaviour of physical systems modelled by
partial differential equations through the choice of boundary data. Recent
interests are centered on vibrating flexible systems.
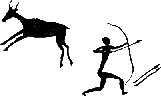
-
Optimization
(Sanjo Zlobec,
Neville
Sancho, J.-L. Goffin):
The figure on the right was discovered in a cave in Spain. It is about 13
millennia old and it depicts the oldest optimization problem we are aware
of. The range of the caveman's arrow depends on the projection angle
(parameter). The problem of determining the angle that yields the maximal
range, subject to the gravitational force, can be formulated and studied as
a stable convex parametric programming model. The parallel arrows on the
right of the caveman appear to depict the solution (optimal projection
angle). In a modern version of this problem, a businessman wants to
determine prices of products, subject to economics constraints, that yield
the maximal profit. Problems like these can be formulated and solved as
mathematical programming (optimization, parametric) models.
-
Dynamical Systems (Tony Humphries):The
image
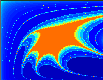 you see on the left is the attractor of a simple discrete dynamical
system arising when one tries to solve a system of ordinary
differential equations describing the evolution of a prey and a
predator in a common habitat. The exact solution is known to be
cyclic, so the numerical scheme should have this property as well.
Inside the orange area the chosen numerical scheme has this property,
outside it becomes useless. But what is the structure of the boundary
?
you see on the left is the attractor of a simple discrete dynamical
system arising when one tries to solve a system of ordinary
differential equations describing the evolution of a prey and a
predator in a common habitat. The exact solution is known to be
cyclic, so the numerical scheme should have this property as well.
Inside the orange area the chosen numerical scheme has this property,
outside it becomes useless. But what is the structure of the boundary
?
Research Seminars





 Computational Electromagnetics
(Nilima Nigam): The image shows a finite element
simulation of a cavity problem. If you click on the image, the triangular mesh is clearly visible;
the quantity plotted is the electric potential for a cavity with an inclusion of different
electrical properties.
Computational Electromagnetics
(Nilima Nigam): The image shows a finite element
simulation of a cavity problem. If you click on the image, the triangular mesh is clearly visible;
the quantity plotted is the electric potential for a cavity with an inclusion of different
electrical properties.

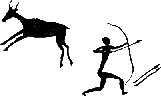
 you see on the left is the attractor of a simple discrete dynamical
system arising when one tries to solve a system of ordinary
differential equations describing the evolution of a prey and a
predator in a common habitat. The exact solution is known to be
cyclic, so the numerical scheme should have this property as well.
Inside the orange area the chosen numerical scheme has this property,
outside it becomes useless. But what is the structure of the boundary
?
you see on the left is the attractor of a simple discrete dynamical
system arising when one tries to solve a system of ordinary
differential equations describing the evolution of a prey and a
predator in a common habitat. The exact solution is known to be
cyclic, so the numerical scheme should have this property as well.
Inside the orange area the chosen numerical scheme has this property,
outside it becomes useless. But what is the structure of the boundary
?