>	with(linalg):

Warning, the protected names norm and trace have been redefined and unprotected

>	#We consider again the matrix

>	A:=matrix([[1, -1, 0, 0, 0, 0], [4, 5, 0, 0, 0, 0], [0, 0, 0, -1, 0, 0], [0, 0, 1, 0, 0, 0], [0, 0, 0, 0, 0, 1], [0, 0, 0, 0, -1, 0]]);

>	factor(minpoly(A, t));

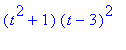
>	#We now consider the Primary Decomposition Theorem over the rational numbers. Previously we have factored (t^2+1) = (t+I)(t-I) and dealt with linear factors. Over Q, (t^2+1) is irreducible. The corresponding subspace is

>	W1:=kernel(A^2+1);

>	#In addition we have

>	W2:=kernel((A-3)^2);

>	#The change of basis matrix is

>	M:=transpose(matrix([W1[1], W1[2], W1[3], W1[4], W2[1], W2[2]]));

>	#We change basis and get

>	multiply(inverse(M), A, M);

>	#Notice the matrix is indeed composed of two blocks (4x4 and 2x2).