M
C
G
I
L
L

M
A
T
H
E
M
A
T
I
C
S
 

M
C
G
I
L
L

M
A
T
H
E
M
A
T
I
C
S
 

M
C
G
I
L
L

M
A
T
H
E
M
A
T
I
C
S
 

M
C
G
I
L
L

M
A
T
H
E
M
A
T
I
C
S
 

M
C
G
I
L
L

M
A
T
H
E
M
A
T
I
C
S
 

M
C
G
I
L
L

M
A
T
H
E
M
A
T
I
C
S
 

M
C
G
I
L
L

M
A
T
H
E
M
A
T
I
C
S
 

M
C
G
I
L
L

M
A
T
H
E
M
A
T
I
C
S
 

M
C
G
I
L
L

M
A
T
H
E
M
A
T
I
C
S
 

M
C
G
I
L
L

M
A
T
H
E
M
A
T
I
C
S
Algebraic Geometry
 

Algebraic geometry is one of the oldest and vastest branches of mathematics. Besides being an active field of research for many centuries, it plays a central role in number theory, differential geometry, group theory, mathematical physics and other branches of science.
 

In McGill, algebraic geometry is represented by Peter Russell and Eyal Goren and is very much connected to the interests of other members of the department: Henri Darmon, Jacques Husrtubise and Niky Kamran. We are running a joint seminar with CICMA, Université de Montreal and UQAM. In addition there are courses given in algebraic geometry and related areas. Check it out!

Activities in Algebraic Geometry.


 
 

What is Algebraic Geometry?

Initially, algebraic geometry was concerned with the study of curves in the plane and really started boosting up with the discovery of projective geometry. In this geometry, the line k (k any field) is completed by adding one point at infinity resulting in the projective line P1, the plane k2 is completed by adding a projective line at infinity to yield the projective plane  P2. Thus P2= k2U P1=k2 U k U{pt}. 

 
On a more conceptual level, the projective space Pn over a field k is the parameter space of lines in kn+1. Such a line is determined by a non-zero point on it (a0, ... , an), where one is allowed to replace (a0, ... , an) by (ta0, ... , tan) for any non -zero t in k. We denote such a class of points by (a0: ... : an). Thus Pn is the collection of (a0: ... : an). The points with a1 not equal to 0 may be normalized so that a1 = 1. Then a1, ... , anin (1: a1: ... : an) are determined uniquely and are in one to one correspondence with kn by the map (1: a1: ... : an)  ---> (a1, ... , an). The complement is the points (0: a1: ... : an), which are precisely Pn -1 . Thus we get an inductive dissection Pn = kn U kn-1 U ... U k  U {*}, where * is the point (0: ... :0:1). 
 
One of the nicest theorems is
 
Bezout's theorem: Two curves C and D in P2, defined by equations of degree M and N intersect at MN points, counting multiplicity.
In particular, every two lines intersect at a unique point. This last fact was in fact one of the drives to develop projective geometry. It came from the invention of perspective in art and architecture. Invention whose roots are in the world around us:

 
For long time geometry was the study of projective geometry. By that one means the study of sets defined as the set of solutions for a given system of homogeneous polynomials. Such sets look like a set Y in kn such that the points of Y are the common solutions to a system of polynomials (f1, ... , fr) in n variables, and where one adds to Y its limit points at infinity. 
One is interested in intrinsic properties of such sets, properties not depending on metric and coordinates. Properties like dimension, singular points and others. In fact, a characteristic research problem is finding such intrinsic properties. 
 
Much effort went into freeing algebraic geometry from the necessity of dealing with sets defined by a particular collection of equations. This was to serve not only for solving some technical problems at the time, but also to signal out precisely what are the objects of study to themselves before we incorporate them in any particular way into a space. This is very similar to the way manifolds are studied today via the definition of atlas. 
 
Another problem was to find a way of actually saying what is geometry. One can think about geometry as a collection of objects, where for any two objects it is known whether "one lies on the other", and where it is known what is a regular function on such a structure. 
 
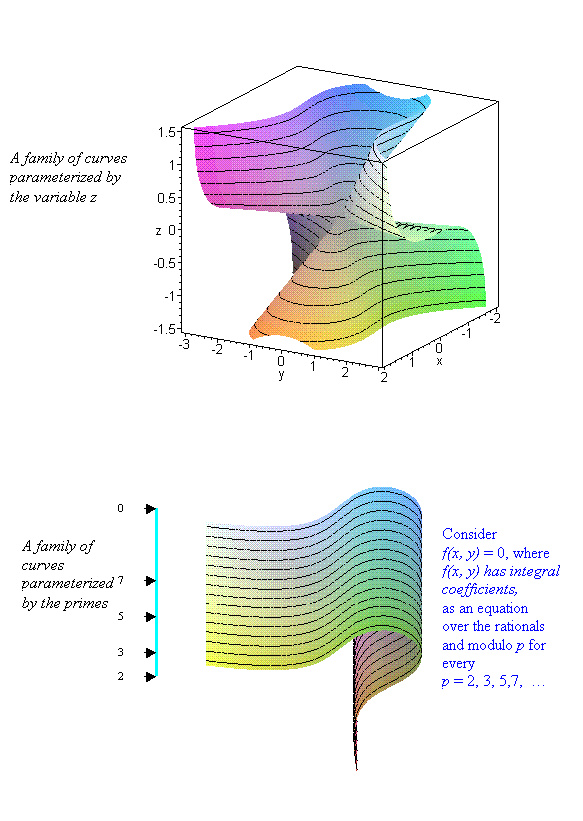
Yet another problem is putting on a firm ground the "feeling" that a family of algebraic sets (say a family of curves) varying smoothly in time is "like" a curve defined using equations with integer coefficients where for every prime number one can consider the curve modulo this prime. Hence the curve varies over the parameter space whose points are primes.
All these problems, and many other problems coming from the attempt to generalize known results in complex geometry to results in algebraic geometry, lead to the development of modern algebraic topology. The chief inventor and force behind which was Grothendieck with many deep contributions by Dieudonné, Serre, Deligne and many others.
In this theory of schemes, the basic objects are composed of rings. The objects of the geometry are the prime ideals of the ring and the notion of "lying on" is given by "containing". The functions are given by elements of the ring itself. Mysterious as itseems, this makes for a totally coherent geometric theory, where such spaces (called "spectra") can be glued together, and where any classical geometric notion can be defined.
Today, algebraic geometry is composed of many different branches. Some are closely related to complex analysis (geometry over the complex numbers), some are closelyrelated to number theory (moduli spaces), some to mathematical physics (Calabi-Yau manifolds and mirror symmetry), some to algebraic topology (elliptic cohomology, étale cohomology, topoi) etc. 
Apart from those, as any developed branch of science, algebraic geometry is troubled with its own house keeping: How many curves of a degree 3 pass through 9 points in the plane? How many lines are there on a cubic surface? How to parameterize all the varieties in Pn of some given invariants? How to understand group actions on a given
space and existence of a quotient? What is the structure and properties of algebraic groups? What do the automorphisms of an algebraic variety look like? etc.,  etc...

 

Members of the department studying algebraic geometry are Peter Russell and Eyal Goren. Members whose interests are bordering with algebraic geometry are Niky Kamran, Jacques Hurtubise, Henri Darmon and many of the members of CICMA.
 
 
 
 

Individual research interests:
 

Eyal Goren:  I am interested in questions where number theory is studied via geometry. Specific key words are modular forms, moduli spaces, elliptic curves, abelian varieties, p-divisible groups, L functions.

In the last couple of years I was working on the ambitious project of bringing our knowledge of moduli spaces of abelian varieties and modular forms on them to the level of our knowledge in the case of elliptic curves. Here we comment that an abelian variety is a complete algebraic group (over C it is topologically a torus) and the moduli space is a variety that parameterize all those abelian varieties. Every variety gives a point in the space and a curve C in the moduli space gives a family of abelian varieties parameterized by C.

 
In the case of elliptic curves this theory played a crucial role in the proof of Fermat's last theorem. It is therefore expected that much deep mathematics is to be discovered in the study of such moduli spaces, connecting questions from number theory (in particular Diophantine equations and modular forms) to questions on the geometry of these moduli spaces.
Specific questions I have been working on together with E. Bachmat and F. Oort are the geometry of Hilbert modular varieties in positive characteristic (stratification, variation of Newton polygons, singularities), p-adic and mod p Hilbert modular forms and p-divisible groups with real multiplication.

 

Peter Russell:  I have long been interested in studying affine spaces and closely related varieties (e.g., over C, contractible affine varieties) as algebraic varieties in their own right. The famous cancellation problem, for instance, asks whether X is an affine space provided that X x C is an affine space. This is known if the dimension of X is at most 2.

Closely related is the quest to understand the automorphism group of affine space Cn, still a mystery for n bigger than 2. A quite recent result (obtained in collaboration with M. Koras and others) says that C* actions on C3 are linear in a suitable coordinate system. Again, this is not known for Cn, n >3. 

Among my other interests are the study of embeddings of rational curves in the affine plane (generically rational curves, closed embeddings of C*, ...); some special topics in positive characteristic geometry (purely inseparable forms, Frobenius sandwiches, ...).
 
 
 
 
 

Activities in Algebraic Geometry
 

Courses (current and recent years): 

1997-1998: 
Commutative algebra and algebraic geometry (Algebre 1). UdM. MAT 6608. Lecturer: B. Broer. Automn 97. 

Topics in Algebra III: Approaches to the Jacobian Problem. McGill. 189-722A. Lecturer: A. Sathaye. 
 

1998-1999: 
Algebraic surfaces. McGill University. 189-725A. Lecturer: P. Russell. (A semester course leading to the study of systems of curves on an algebraic surface and the notion of Kodaira dimension for compact and non-compact surfaces). 

Algebraic Curves. McGill. 189-612B. Lecturer:J. Hurtubise.
 

1999-2000: 
Topics in Geometry and Topology. McGill University. 189-706A/707B. Lecturer: E. Goren. (A year long course in algebraic geometry, from classical theory to schemes. The course is aimed at the graduate, or advanced undergraduate level.  Pre-requisites are some basic algebra and topology. For more details go here. )

2000-2001:
Introduction to Riemannian symmetric spaces. (Topics in Geometry and Topology I). McGill 189-706A, MW 10:30 - 12:00, Room 1214. Lecturer: F. Andreatta.  The course is aimed at the beginning graduate student level and higher, and is open to advanced undergraduate students. After introduction of the necessary background in differential geometry and Lie theory, the focus would be the notion of symmetric spaces, their properties, their relation and classification in terms of Lie groups due to Cartan. Applications and connections to number theory and arithmetic algebrai geometry (e.g. classification of variations of Hodge structures, Shimura varieties) would be given in detail depending on time. 
           
Elliptic Curves (Topics in Algebra). Concordia MAST 699I/4. Lecturer: Chantal David. This course will cover the basic theory of elliptic curves and algebraic curves. The recommended textbook is: The arithmentic of elliptic curvesby J. Silverman. The prerequisites for this course are part of the standard background in abstract algebra (groups, rings, field extensions etc). A
first course in algebraic number theory is also recommended. The course is open to all graduate students, either at the master or the Ph.D. level.
 

COMING YEAR (2001-02):

Introduction to Algebraic Geometry. Lecturer: E. Goren.  This is an introductory course in Algebraic Geometry. It develops from scratch the theory of algebraic varieties over algebraically closed fields, including morphisms, sheaves and cohomology. The course presupposes basic commutative algebra. The topics to be studied are: affine and projective algebraic
varieties; regular functions and morphisms; singularities, normalization and blow-up; sheaves, Cech cohomology and the
Riemann-Roch theorem for curves. The examples of curves, and Grassmannian manifolds are studied in detail.

Vecotr bundles on Curves. Lecturer: E. Goren.  This is a special graduate course given within the Theme Year on Groups and Geometry taking place at the CRM during 2001-02. The course presupposes basic algebraic geometry at the level of the course \emph{Introduction to Algebraic Geometry} given in the first term. It develops the theory of curves and vector bundles of curves and their moduli. The topics to be studied are: curves, the Riemann-Roch theorem and the Hurwitz genus formula; vector bundles on curves and their invariants, monodromy, flat vector bundles and Weil's theorem; semi-stability; the Hilbert scheme; geometric invariant theory; construction of moduli spaces.
 
 

Seminars

Algebraic Geometry Seminar. 

Quebec-Vermont Number Theory Seminar.

graduate students seminar. 

See also the activities of

CICMA
 

 


Page  constructed by Eyal Goren: goren@math.mcgill.ca