A simple definition of Geometric group theory is that it is the study of groups as geometric objects.

Thinking about groups this way was popularized by Gromov who revolutionized the subject of infinite groups. This is a new field, so there are many fundamental theorems waiting to be discovered, and it is a rich field, lying at a juncture between algebra and topology, where a great variety of methods from other branches of mathematics can be utilized. Geometric group theory draws upon techniques from, and solves problems in the theory of 3-manifolds, hyperbolic geometry, combinatorial group theory, Lie groups...

The simplest way of regarding a group as a geometric object is through its "Cayley Graph".
Consider a finitely generated group G with generators s₁, s₂,  ... , s_n. This just means that every element of G can be expressed as a product of the s_i  elements and their inverses. The Cayley graph of G is a graph whose vertices are precisely the elements of G, and whose edges are described by the rule that  for each pair of elements x, y of G there is an edge labeled by  the generator s_i which originates at x and terminates at y provided that xs_i = y .

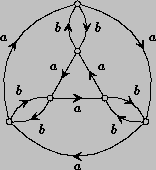An elementary example is the Cayley graph of the dihedral group D₃, which is the group of symmetries of an equilateral triangle. Of course, the Cayley graph depends on the choice of generators. In this case we are using a generator a which is a 120 degree rotation, and a generator b which is a reflection.

When the group G is infinite, its Cayley graph reflects large-scale geometric features which can have a profound effect on the algebra of G. Techniques which are reminiscent of topology and Reimannian geometry can be brought to bear, and they can reveal deep properties of the group which are hidden to combinatorial and algebraic investigation.