Calculus 1 Science

Final Exam

Winter 1999 Semester

Numbers in square brackets [ ] are mark values

1. Evaluate the limits visually from the respective graphs. If the limit does not exist state in which

way (or "does not exist".)

y=f(x)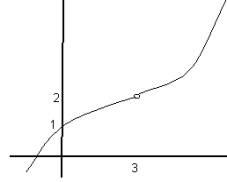

y=g(x)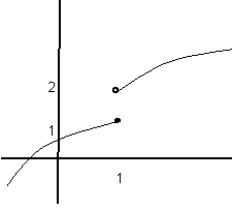

y=h(x)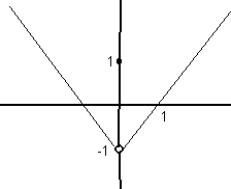

[3] a) (i) (ii) iii)

[2] b) Using the above functions, also find,

(i) (ii)

[1each] 2. Evaluate the following limits. If the limit does not exist state in which way (or "does not exist".)

[2] 3. Evaluate . If you use a calculator, make sure it is in radian mode.

[2] 4.a) State the conditions under which a function f (x) is continuous at x=c.

[2] b) Is g(x) continuous at x=1? Justify your answer.

[1] 5. a) State the limit definition of the derivative.

[3] b) Use the limit definition of the derivative to find f '(x) if .

[3 each] 6. Find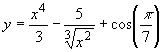 for each of the following functions. Do not simplify.

[3] 7. Find if .

[4] 8. Find the equation of the tangent line to the curve at x=1.

[4] 9. Given , find y''.

[5] 10. Sketch the graph that satisfies these conditions.

when x<-3

when -3<x<-1

when x>-1

when -3<x<2

when x>2.

[6] 11. Sketch the following graph showing all steps. Label all intercepts, relative extrema, inflection points and horizontal and vertical asymptotes. State the intervals on which the function is increasing, decreasing, concave up, and concave down.

[5] 13. A ball is thrown straight upward from the earth's surface with an initial velocity of 100 ft/sec (30 meters/sec.). The position of the ball after t seconds is given by feet.

1. Determine the average velocity of the ball between 2 and 3 seconds.
2. Determine the velocity function.
3. What was the instantaneous velocity of the ball exactly 2.5 seconds after it was thrown?

[5] 14. Find the absolute extrema (maximum and minimum) of the function on the closed interval [-3,0].

[3each] 15. Evaluate the following.

[4] 16. Given , find y if y=45 when x=3.

[4] 17. Find the area of the region bounded by the graph of , the x axis, and the lines x=0 and x=5.