Montreal St.-Lawrence River, great Canadian river
Numerical Computation
The following presents some numerical results on the
phase transition problem.
For a 2x2 system of conservation laws with artificial viscosity like
van der Waals's fluid (or viscoelastic dynamics), the pressure (or the
strain function) is non-monotone so that the system with zero viscosity
is mixed. Such a problem exhibits three phases:
water, water-vapor and vapor phase
(or soft material, mixture material and hard material in the case of viscoelasticity),
mathematically, corresponding to
hyperbolic region, elliptic region and hyperbolic region.
Recently, we prove theoretically and numerically that:
1). if the
mean value of the initial integral is in the hyperbolic
region (water phase, or vapor phase), no matter how small the artificial
viscosity is, the global solution uniquely exists and converges to the
mean value of the initial integral. In particular, after a short initial oscillation,
the solution still keeps in the same hyperbolic region, and no phase transition
occurs. See Figure 1.1
2). if the
mean value of the initial integral is in the elliptic
region (water-vapor phase), and the artificial
viscosity is big, the global solution uniquely exists and converges to the
mean value of the initial integral. In particular, after a short initial oscillation,
the solution still keeps in the same elliptic region, and no phase transition
occurs. See Figure 2.1
3). if the
mean value of the initial integral is in the elliptic
region (water-vapor phase), and the artificial
viscosity is small, the global solution oscillates in all time across
three phases. The phase transitions
occur. See Figure 3.1 for 3-D case,
and
Figure 3.2, Figure 3.3,
Figure 3.4, Figure 3.5
for 2-D case at different times.
Numerical Simulations
(click the following small pictures for large)
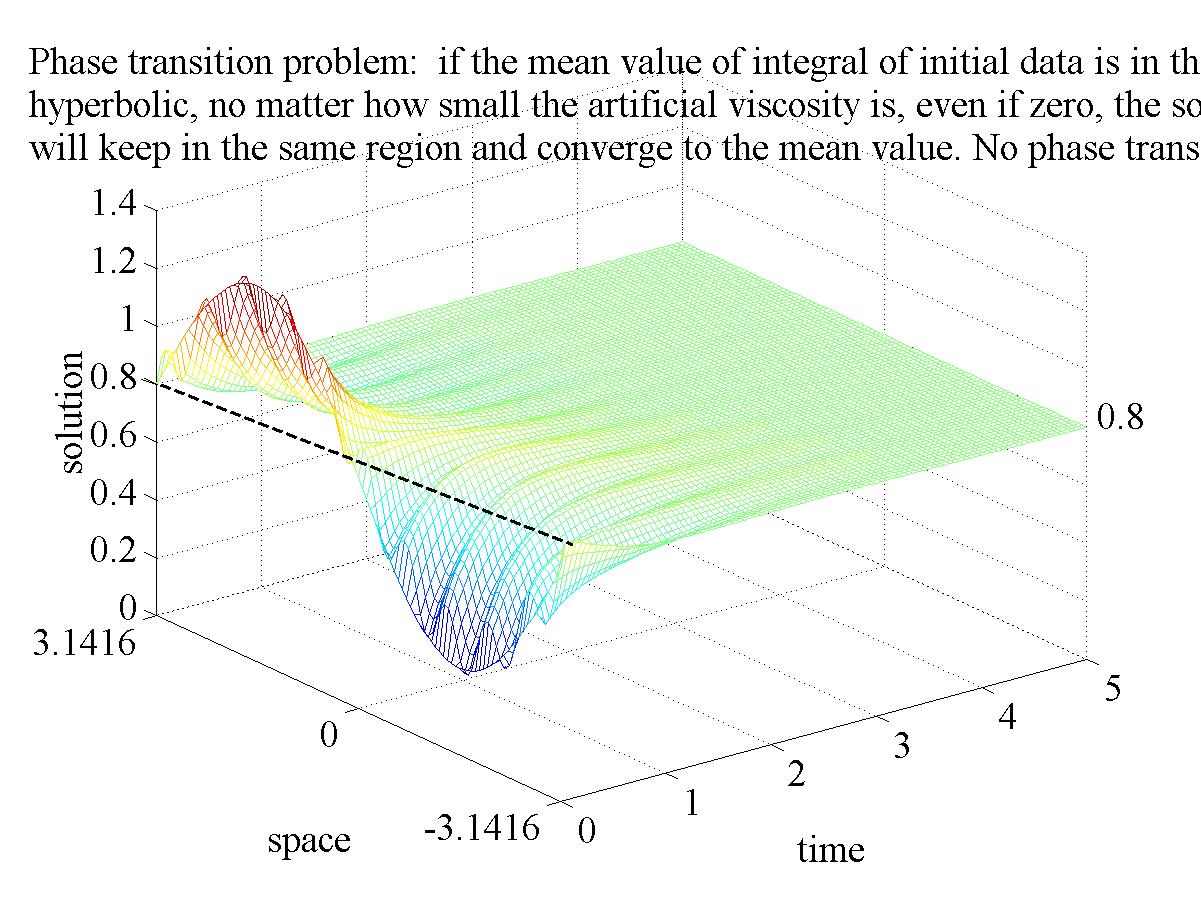Figure 1.1,
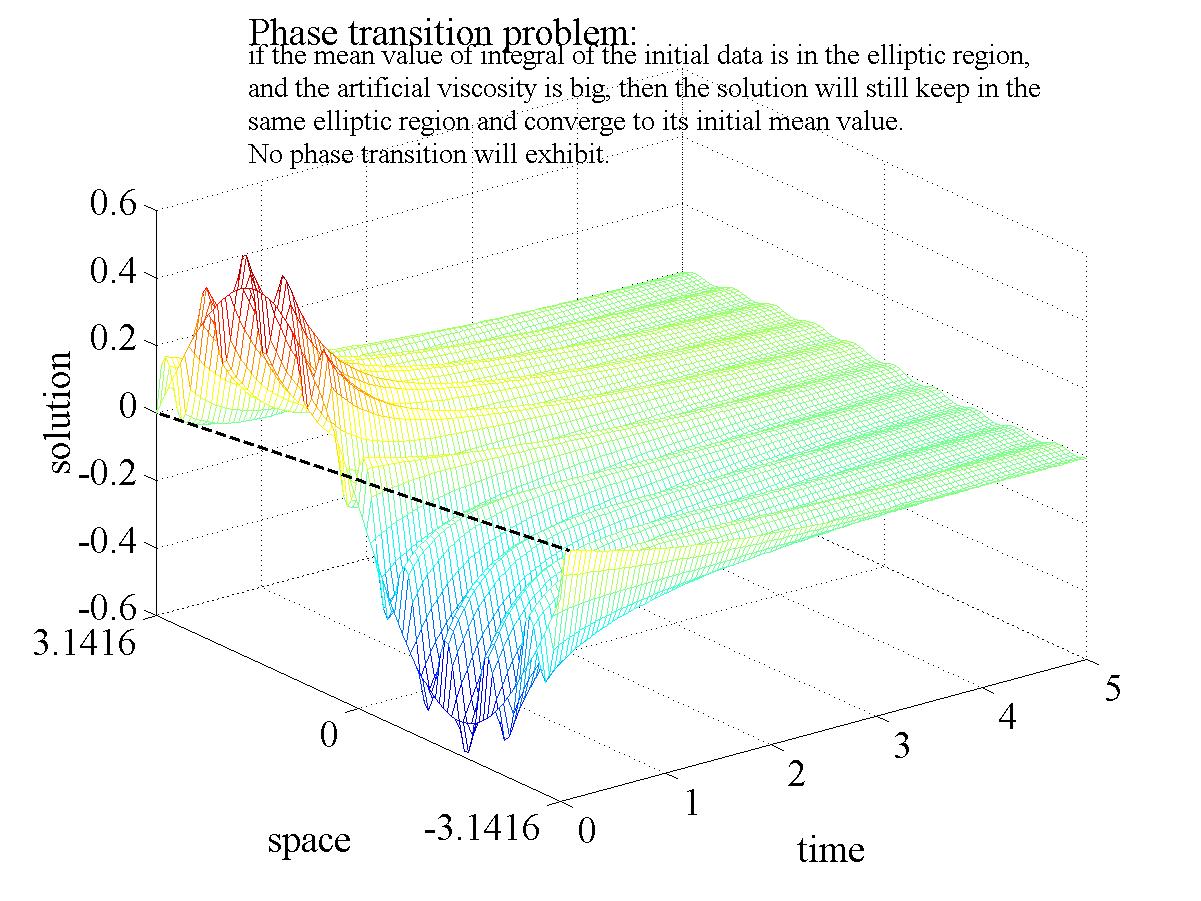Figure 2.1,
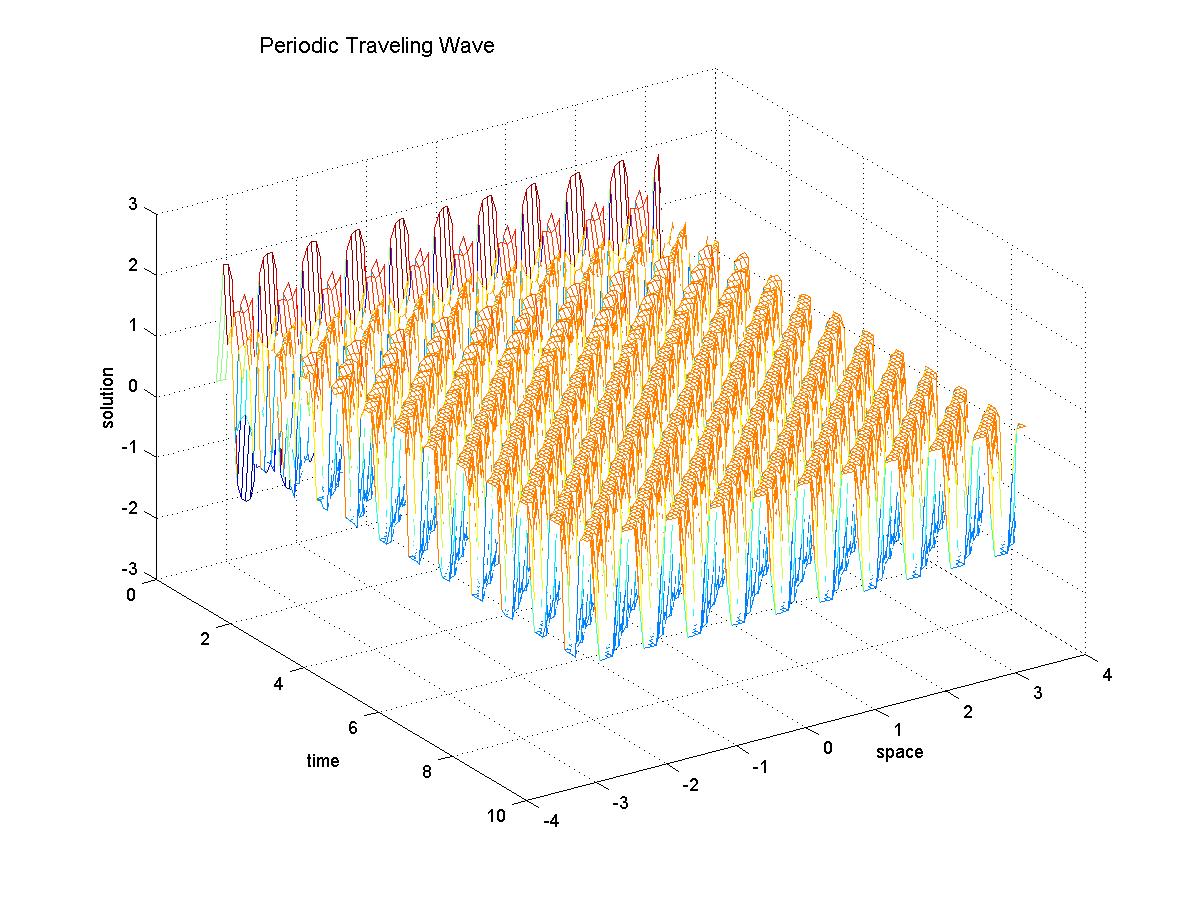Figure 3.1,
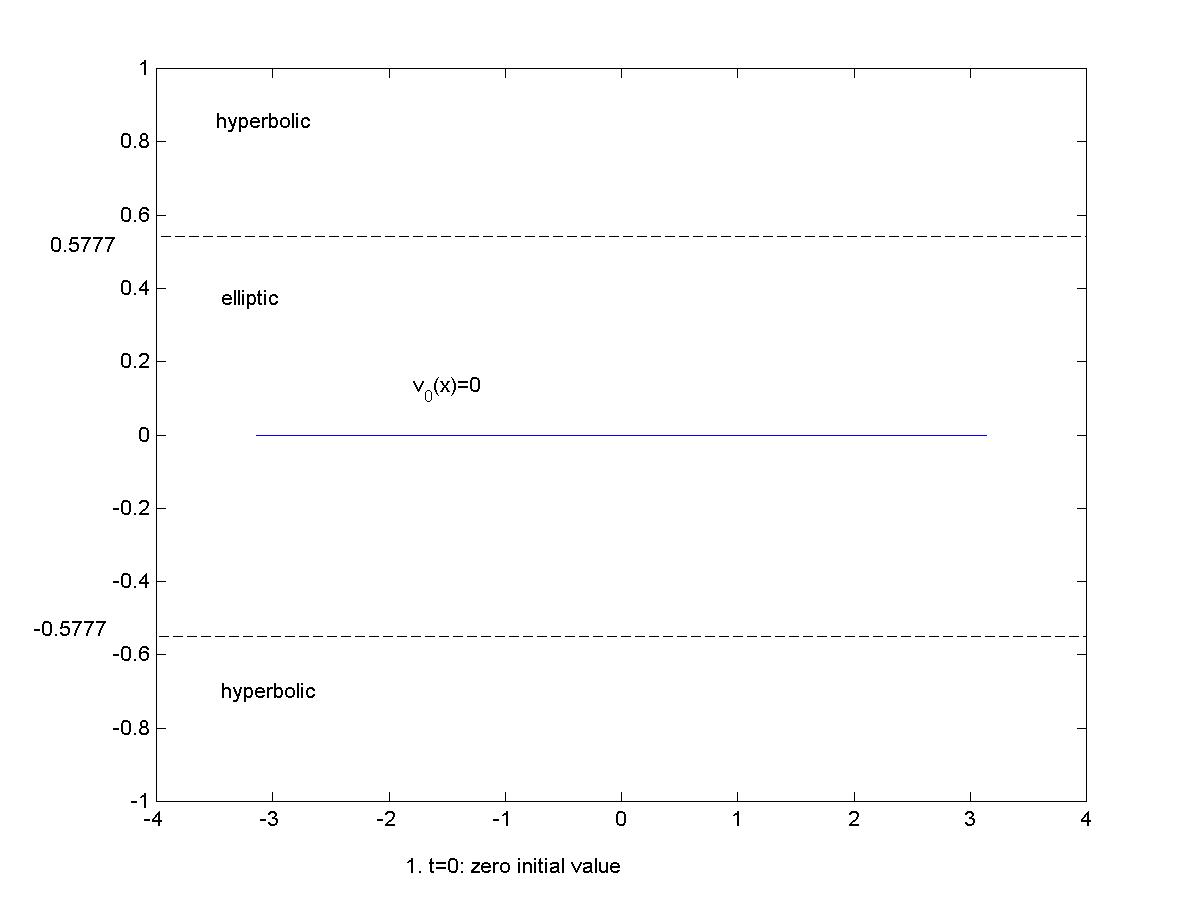Figure 3.2,
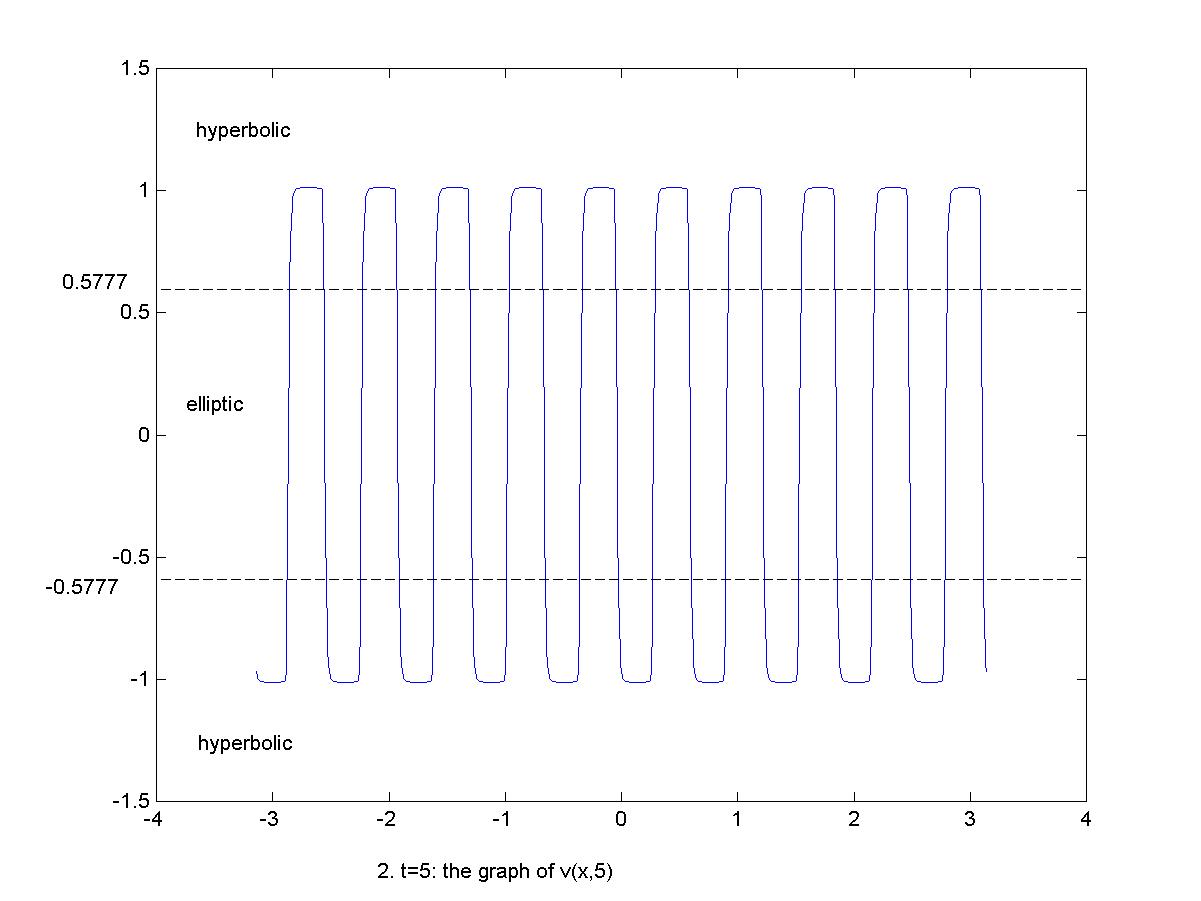Figure 3.3,
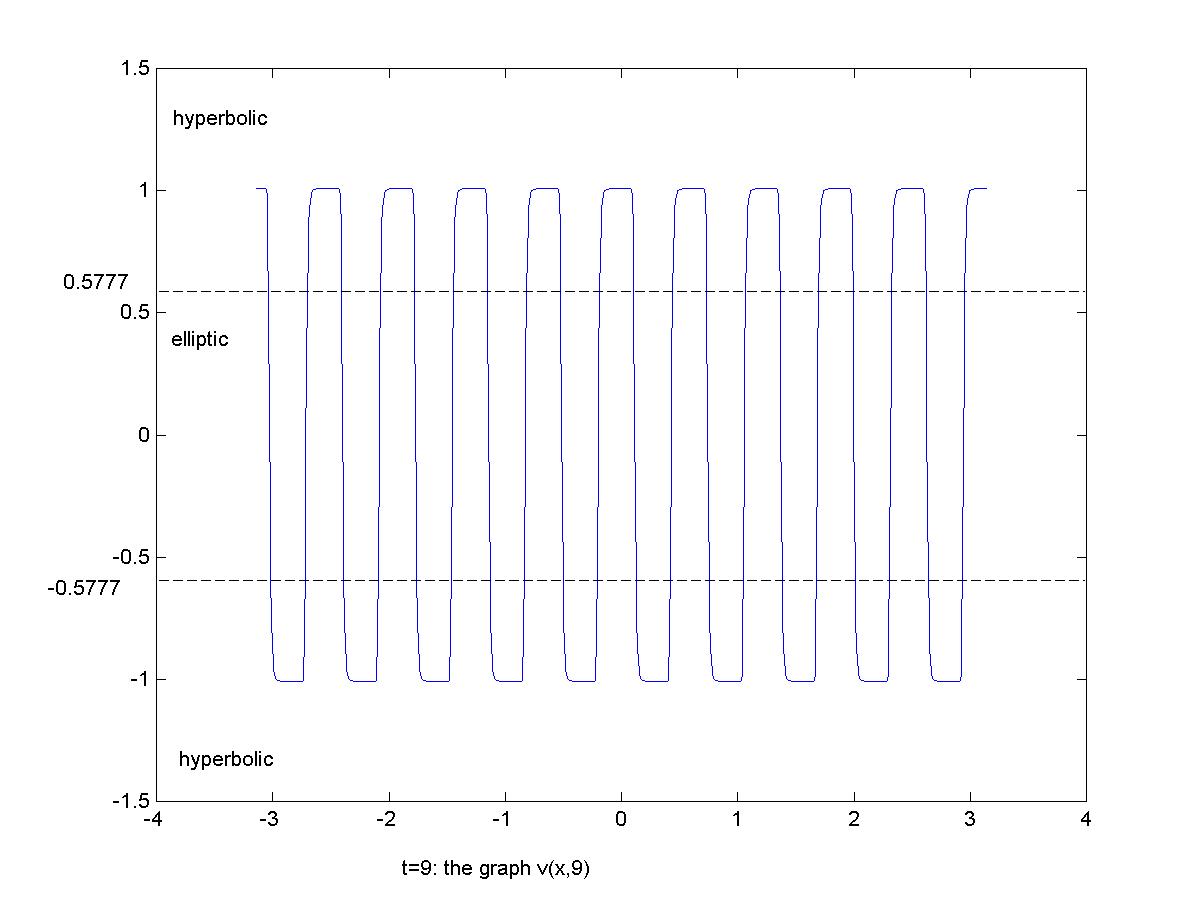Figure 3.4,
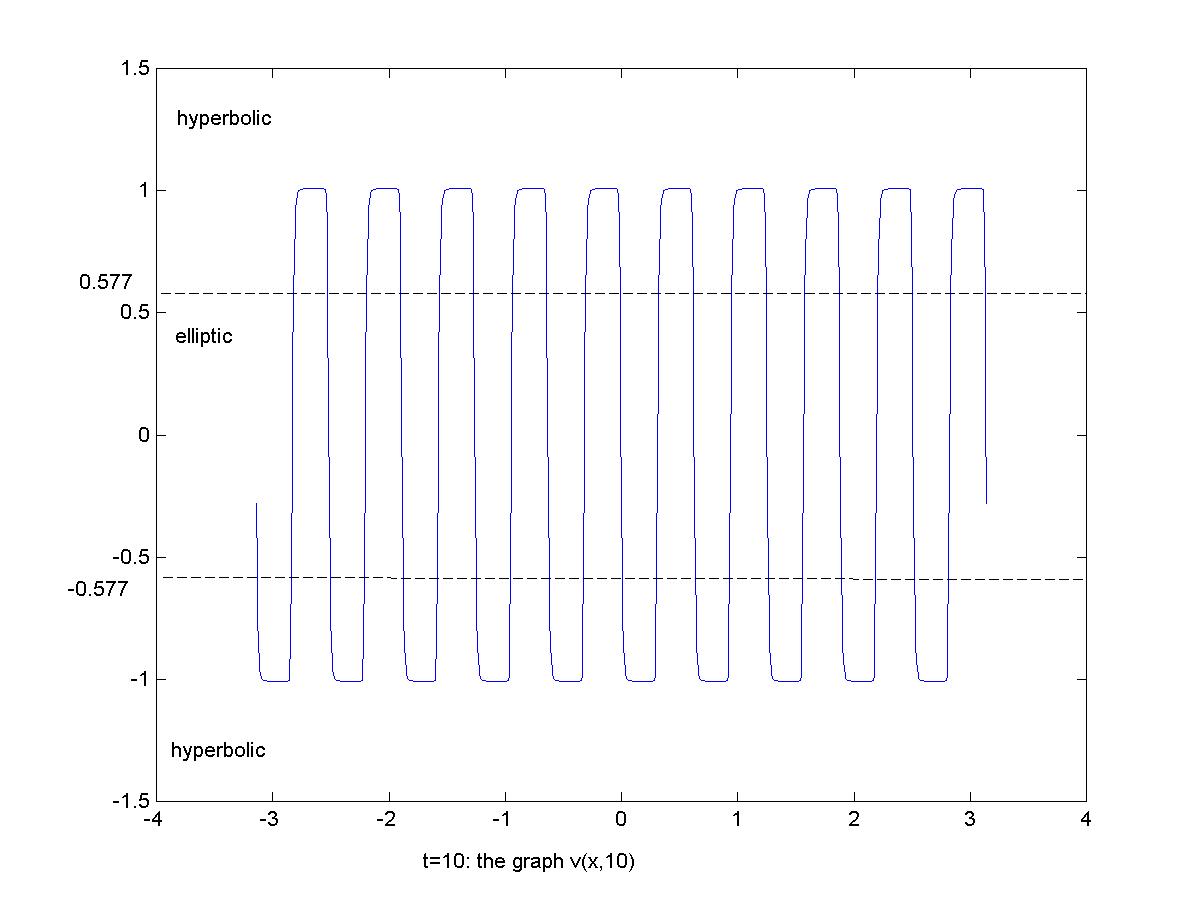Figure 3.5.
Figure 1.1,
Figure 2.1,
Figure 3.1, 
Figure 3.2,
Figure 3.3,
Figure 3.4, 
Figure 3.5.