==== Numerical Analysis: Example in Section 2.3=====
================ by Dr. Ming Mei=============
Question: (Ex. Q.13, page 75)
1. by Method of False Position
> f:=x->230*x^4+18*x^3+9*x^2-221*x-9;
![]()
> plot(f,0..1);
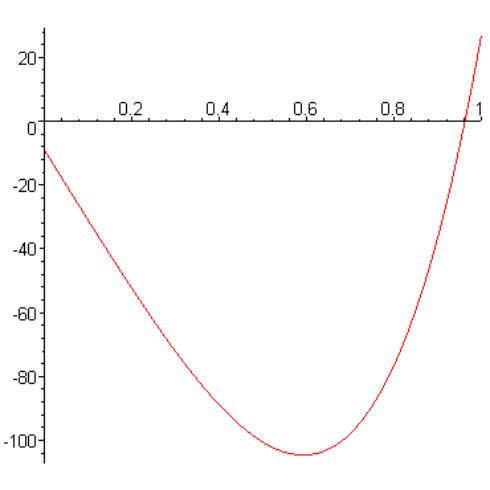
> a:=0; b:=1; i:=1; maxstep:=22; tolerance:=0.000001; err:=100.0;
![]()
![]()
![]()
![]()
![]()
![]()
> for i from 1 to maxstep while (evalf(err)>tolerance) and (abs(b)<10000) do p:=evalf(b-f(b)*(b-a)/(f(b)-f(a))); err:=abs(b-p);
> if evalf(f(b)*f(p)<0) then a:=p else b:=p end if;
> ans:=p; print("answer=",ans,"error=", evalf(err), "step=",i);
> end do;
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
2. by Secant Method
> restart;
> f:=x->230*x^4+18*x^3+9*x^2-221*x-9;
![]()
> a:=1/2; b:=1; i:=1; maxstep:=22;
tolerance:=0.000001; err:=100.0;
# select a proper initial
approximation is very
# important. Try a=0 to see what a
numerical result
# you might have.
![]()
![]()
![]()
![]()
![]()
![]()
> for i from 1 to maxstep while (evalf(err)>tolerance) and (abs(b)<10000) do p:=evalf(b-(f(b)*(b-a))/(f(b)-f(a))); err:=abs(b-p); a:=b; b:=p; ans:=p; print("answer=",ans,"error=", evalf(err), "step=",i);
> end do;
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
===============================================================
3. by Newton's Method
> restart;
> f:=x->230*x^4+18*x^3+9*x^2-221*x-9;
![]()
> df:=D(f);
![]()
> a:=1; i:=1; maxstep:=22; tolerance:=0.000001; err:=100.0;
![]()
![]()
![]()
![]()
![]()
> for i from 1 to maxstep while (evalf(err)>tolerance) and (abs(a)<10000) do p:=evalf(a-f(a)/df(a)); err:=abs(a-p); a:=p; ans:=p; print("answer=",ans,"error=", evalf(err), "step=",i);
> end do;
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()