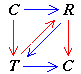
I first recalled a bit from last week's talk, for the benefit of people who didn't attend that talk and as a refresher for the others. Then, I showed that the pasting scheme whose cells are n-dimensional (p,q)-shuffles has no direct loops, and I introduced a rank function, which basically measures how far 0's are from being up front and 1's are from being down rear, with a twist to take into account the places and the parity of the swaps. Eventually, I will use induction over the rank in proofs of well-formedness statements.
See sections 4-5 of the paper ``The shuffle pasting'' (in preparation).