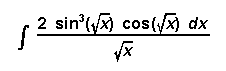
203 S Calculus 2

[numbers in square brackets are marks]

(1) Perform the following integrals:

[5] ( a)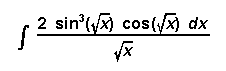

[5] ( b)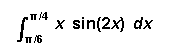

[5] ( c)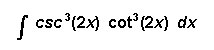

[5] ( d)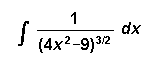

[5] ( e)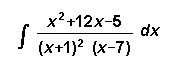

[4] ( f)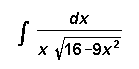

(2) Calculate the following limits:

[4] ( a)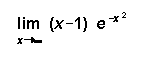

[4] ( b)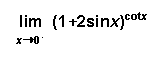

(3) Determine if the following integrals converge or diverge:

[4] ( a)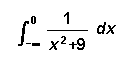

[4] ( b)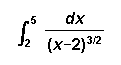

[6] (4a) Find the volume of the solid of revolution obtained by rotating the region bounded by the curvesandabout the x-axis. Indicate which method you are using.

[4] (4b) Find the area of the region.

[4] (5) Find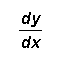and simplify:

(6) Determine whether the following series converge or diverge. State the test used and show that the conditions of the test have been met.

[5] ( a)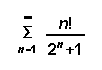

[5] ( b)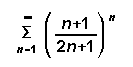

[5] ( c)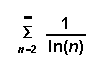

[5] ( d)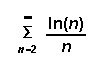

(7) Determine whether the following series as absolutely convergent, conditionally convergent, or divergent.

[5] ( a)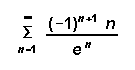

[5] ( b)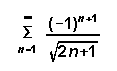

[6] (8) Find the interval of convergence for: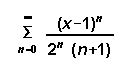

[5] (9) Find the first three non-zero terms of the Taylor series forabout.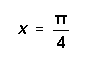



Answers