Calculus 2 for Science Final Exam Fall 1997 Numbers in brackets() are mark values.
(3) 1. Differentiate:
![]()
![]()
![]()
2. Evaluate the following integrals:
(3) a) ![]()
(4) ![]()
(5) c) 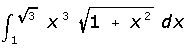
(5) d) ![]()
(5) e) ![]()
![]()
![]()
(5) f) ![]()
(5) g) 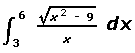
(5) h) ![]()
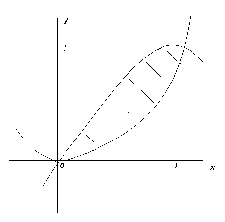
3. Consider the shaded region
bounded by ![]() and
and
![]() , between
, between ![]() and x = 1.
and x = 1.
(3) a) Find the area of this region.
(5) b) Find the volume of the solid generated by revolving this region about the x-axis. [Use the
"ring"/"washer" method.]
(2) c) Set up the integral, BUT DO NOT EVALUATE IT, for the volume of the solid generated by revolving this region about the y-axis.
4. Evaluate the following limits:
(3) a) ![]()
![]()
(3) b) ![]()
![]()
(3) c) ![]()
5. Determine divergence or convergence (and evaluate if convergent) for the following integrals:
(5) a) ![]()
(3) b) ![]()
6. Consider the sequence defined by ![]()
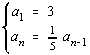
(1) a) Write the first four terms:
a1 =
a2 =
a3 =
a4 =
(1) b) Write an expression for the nth term of this sequence that is not a recursive definition.
(1) c) Compute ![]()
(2) 7. Determine whether the given geometric series converges or diverges. If the series
converges, find its sum.
![]()
8. Determine whether the following series converge![]() or diverge. State which test you are using,
and show that any conditions for the application of the test have been met.
or diverge. State which test you are using,
and show that any conditions for the application of the test have been met.
(3) a) 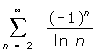
(3) b) 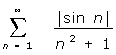
(3) c) 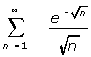
(3) d) 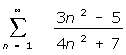
(3) 9. Do the following series converge absolutely, converge conditionally, or diverge? Justify
your conclusions.
a) 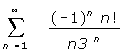
(3) b) 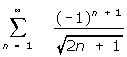
(6) 10. Determine the interval of convergence for the power series
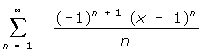
11. Use the Maclaurin series:
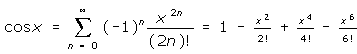 +
+
(2) a) to find the Maclaurin series for ![]()
(2) b) to approximate![]() with an error < 0.001 .
with an error < 0.001 .
____
100