Calculus 1 Winter 1997
[6] (1) Refer to the sketch below to answer the following questions.
If a limit does not exist, state in which way (+ infinity, - infinity,
or "does not exist").
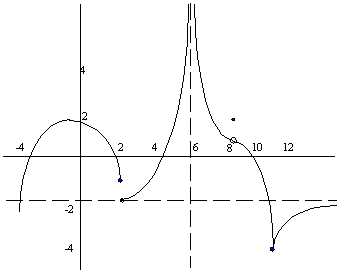
(a) ![]() ____ (b)
____ (b) ![]() ____
____
(c) ![]() ____ (d)
____ (d) ![]() ____
____
(e) ![]() ____ (f)
____ (f) ![]() ____
____
(g) ![]() ____ (h)
____ (h) ![]() ____
____
(i) ![]() ____ (j)
____ (j) ![]() ____
____
(k) ![]() ____
____
(l) _____ is one value of x for which f is continuous and at the same time f is not differentiable.
[10] (2) Use algebraic techniques to calculate the following limits. If an answer is undefined, assign the symbol + or - if possible.
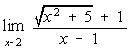
b) ![]()
![]()
![]()
![]()
[3]
(3) (a) Compute the table below for ![]()
|
x |
-0.1 |
-0.01 |
-0.001 |
0.001 |
0.01 |
0.1 |
|
f(x) |
(b) Use your results to give ![]() = _________.
= _________.
[4] (4) Given:
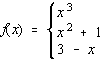
![]()
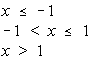
Use the definition of continuity at a point to:
(a) determine whether or not f is continuous at x = -1.
(b) determine whether or not f is continuous at x = 1.
[3] (5) Given: ![]()
(a) Find the equations for all vertical asymptotes for g(x).
(b) Find any other discontinuities for g(x).
[2] (6) Find a value for k which will make f continuous at x = -1.
f(x) = 3 - 2x If x less than or equal -1
f(x) = kx2+2 If x > -1
(7)Consider the formula s(t) = t2 + t in which t is measured in seconds and s(t) is measured in centimetres.
[2] (a) Determine the average velocity from t = 3 to t = 4.
[3] (b) Use a limit definition to find the derivative s'(t).
[2] (c) What is the instantaneous velocity at t = 3?
(8) Give the derivatives of the following functions. Do not simplify your answers.
[3] (a) ![]()
[3] (b) 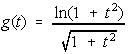
[3] (c) y = sin(2x) sec(3x)
[3] (d) ![]()
[3] (e) ![]()
[4] (f) 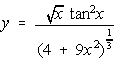 (Use logarithmic differentiation)
(Use logarithmic differentiation)
[4] (9) Find the second-order derivative ![]() for
for ![]() . Do not simplify.
. Do not simplify.
[3] (10) Find all x-values at which the graph of f has a horizontal tangent line.
![]()
(11) Given ![]()
[3] (a) Find: ![]()
[2] (b) Find an equation of the tangent line at (-1, -1).
[3] (12) Find the maximum and minimum values of f on the given closed interval and state where these values occur. Justify your answer.
![]()
[5] (13) A box with a square base and open top must have a volume of 32 000 cm3. Find the dimensions of the box that minimize the amount of material used.
[5] (14) Sketch the graph of a function f having the following characteristics.
![]()
![]() for
for ![]() and for
and for ![]()
![]() for
for![]() and for
and for ![]()
![]() for
for ![]()
![]() for
for ![]()
![]()
![]()
[5] (15) By referring to the graph, complete the chart below by writing in each blank space one of the following symbols: + (positive), - (negative), 0 (zero), or (does not exist).
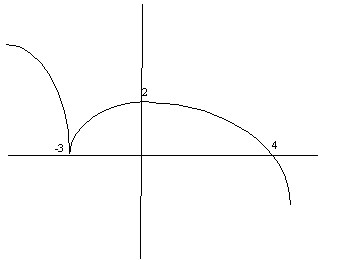
|
x < -3 |
x = -3 |
-3 < x < 0 |
x = 0 |
0 < x < 4 |
|
|
f(x) |
|||||
|
f'(x) |
|||||
|
f"(x) |
(16) Evaluate the following integrals.
[2] (a) ![]()
[2] (b) ![]()
[2] (c) ![]()
[3] (d) ![]()
[3] (e) ![]() Show all work
Show all work
[4] (17) Find the area of the region bounded by the graph of y = 4 - x2 and the x-axis.