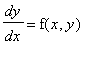
Lecture 8

Text: Sections 1.3, 1.4

Direction Fields. A useful technique that can be used to visualize solutions of the first order DE

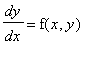
dy/dx = f(x,y)

is the use of the direction field of the equation which consists of a short line segment of slope f(x,y) centered at the point (x,y). For example,

[Maple Plot]

is the direction field of the differential equation

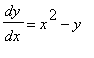dy/dx = x^2-y .

Using this direction field one can sketch solutions of the DE. For example, the solution with y(0)=.5 has the graph

[Maple Plot]

A systematic way to construct the direction field is to draw a short line segment of slope m at various points of the curve f(x,y)=m for a selected range of values of m. These curves are the isoclines for the differential equation 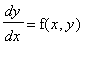dy/dx = f(x,y) . For the above DE the isoclines are the curves y = x^2-m .

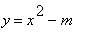The Phase Line. The first order DE 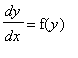dy/dx = f(y) is called autonomous since the independent variable does not appear explicitly. The isoclines are made up of horizonal lines y=f(m). The DE has the constant solution y=m if and only if f(m)=0. These values of m are the equilibrium or stationary points of the DE. The equilibrium point y=m is called a source if f(y) changes sign from - to + as y increases from just below y=m to just above y=m and is called a sink if f(y) changes sign from + to - as y increases from just below y=m to just above y=m; it is called a node if there is no change in sign.Solutions y of the DE appear to be attracted by the line the line y=m if m is a sink and move away if m is a source. The y-axis on which is plotted the equilibrium points of the DE with arrows between these points to indicate when the solution y is increasing or decreasing is called the phase line of the DE.

The autonomous DE 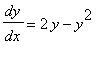dy/dx = 2*y-y^2 has 0 and 1 as equilibrium points. The point y=0 is a source and y=2 is a sink. The direction field of this DE is

[Maple Plot]

This DE is a logistic model for a population having 2 as the size of a stable population. If the population is reduced at a constant rate s>0, the DE becomes

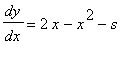dy/dx = 2*x-x^2-s .

which has a source at the larger of the two roots of the equation 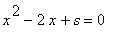x^2-2*x+s = 0 for s<2. If s>2 there is no equilibrium point and the popuation dies out as y is always decreasing. The point s=2 is called a bifurcation point of the DE.