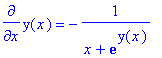
This is a demonstration of the use of Maple to solve and graph the solutions of differential equations.

To solve the differential equation y'=f(x,y) we use the command

dsolve(diff(y(x),x)-f(x,y(x));

The semicolon is obligatory. For example, to solve

> diff(y(x),x) = -1/(x+exp(y(x)));

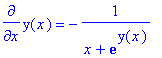
we use the command

> dsolve(diff(y(x),x)+1/(x+exp(y(x))));

and to solve the differential equation

> x*diff(y(x),x)=y(x)^2-y(x);

we use the command

> dsolve(x*diff(y(x),x)+y(x)-y(x)^2);

One can even specify initial conditions

> dsolve({x*diff(y(x),x)+y(x)-y(x)^2,y(1)=2},y(x));

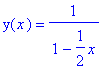
Note that Maple is not perfect as it has not found the zero solution. Even with its deficiencies Maple can solve an impressive list of differential equations, expressing the answers in terms of other well known functions like the Bessel functions which will study later. For example, the differential equation

> diff(y(x),x)=x^2+y(x)^2;

has the general solution

> dsolve(diff(y(x),x)-x^2-y(x)^2);

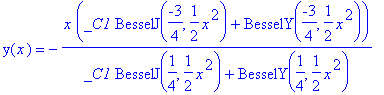
One can even specify the method used to solve an initial value problem. For example,

> with(plots):

> p := dsolve({ diff(y(x),x) = x^2+y(x)^2,y(0)=0 },y(x),type=numeric):

> odeplot(p,[x,y(x)],0..1,labels=[x,y]);

One can also give the direction field for the ODE y'=f(x,y)

> fieldplot([1/sqrt(1+(x^2+y^2)^2),(x^2+y^2)/sqrt(1+(x^2+y^2)^2)],x=-1..1,y=-10..10,arrows=LINE);

>