Jean-Christophe Nave
Associate Professor
McGill University Department of Mathematics and Statistics
Research Areas
Numerical analysis, partial differential equations, level set methods, fluid mechanics, interface problems, multi-phase flows, fluid-structure interaction, computer graphics, applied group analysis / invariant numerical methods, PDE with discontinuous coefficients / discontinuous solutions, computational geometry,...
Education
Ph.D. UCSB 2004 - (Supervisors: Xu-Dong Liu and Sanjoy Banerjee)
History
Associate Professor of Mathematics, McGill Math and Stat Department 2015-present
Assistant Professor of Mathematics, McGill Math and Stat Department 2010-2015
Lecturer of Applied Mathematics, MIT Math Department, 2009-2010
Instructor of Applied Mathematics, MIT Math Department, 2005-2009
Memberships
Steering Committee of the Institut des Sciences Mathematiques 2012-present
Applied Math. Lab. of the Centre de Recherches Mathematiques, 2010-present
CAIMS Membership Committee (register [here]), 2013-present
CNRS-Unite Mixte Internationale CNRS-UMI, 2012-present
Selected Publications
- K. Kamrin, C. H. Rycroft, J.-C. Nave, Reference map technique for finite-strain elasticity and fluid-solid interaction, J. Mech. and Phys. Solids (2012)
[link]
- B. Seibold, R.R. Rosales, J.-C. Nave, Jet Schemes for Advection Problems, Discr. and Cont. Dynam. Syst. - B (2012)
[link]
- A. N. Marques, J.-C. Nave, R. R. Rosales, A Correction Function Method for Poisson problems with interface jump conditions, J. Comp. Phys. (2011) 230
[link]
- J.-C. Nave, R.R. Rosales, B. Seibold, A Gradient-Augmented Level Set Method with an Optimally Local, Coherent Advection Scheme, J. Comp. Phys. (2010) 229
[link]
At McGill
All courses use: [MyCourses]
Winter 2024
Fall 2023
Winter 2023
Fall 2022
Winter 2022
Fall 2021
Winter 2021
Fall 2020
Winter 2020
Fall 2019
Winter 2019
Fall 2018
Winter 2018
Fall 2017
Winter 2017
Fall 2016
Winter 2016
Fall 2015
Winter 2015
Fall 2014
Winter 2014
Quiz #1: Feb. 13th 2014 in class (must be taken in your section).
Quiz #2: March 13th 2014 in class (must be taken in your section).
Quiz #3: April 3rd 2014 in class (must be taken in your section).
Fall 2013
Winter 2013
Fall 2012
Winter 2012
Fall 2011
Winter 2011
Fall 2010
At MIT
Spring 2010
Spring 2009
Spring 2008
Winter 2008
Fall 2007
Spring 2007
Spring 2006
Research Group
PostDocs:
- None
Graduate Students (thesis):
- Damien Tageddine (Ph.D. Candidate)
- Mathieu Cadiot (Ph.D. Candidate) -- (co-supervised with J.-P. Lessard)
- Seth Taylor (Ph.D. Candidate) -- (co-supervised with Gantumur Tsogtgerel)
- Jack Tisdell (Ph.D. Candidate) -- (co-supervised with R. Choksi)
- Manuel Bolduc (M.Sc. ) -- (co-supervised with R. Choksi)
Undergraduate Students:
- Yuki Zhang (B.Sc.Math 2020) [web]
- Noah LeFrancois (B.Sc.Physics 2020) [web]
- Florian Seefeld (B.Sc. Honours Math./Phys. 2021) [web]
- Manuel Bolduc (B.Sc. Honours Math./Phys. 2020) [web]
- Shenshun Yao (B.Sc. Honours Math 2019) [web]
Undergraduate Students:
Visitors:
- Prof. Pascal Poullet (Univ. Antilles) - August 2015 to July 2016
- Prof. Francois Blanchette (UC Merced) - January 2014 to June 2014
- Dr. Alexandre Marques (then at Embraer - now at MIT) - March 2014
Group Alumni
- Dr. Yann-Meing Law (Post Doc - Ph.D. Polytech. Montreal '18) [web]
- Dr. Andy Wan (Post Doc - 2014-2018 - Ph.D. Polytech. Montreal '14) [web] -- Now at University of Northern British Columbia
- Dr. David Shirokoff (Post Doc. - 2011-2014 - Ph.D. MIT '11) [web] -- (co-supervised with R. Choksi)
-- - Now at NJIT
- Dr. Dmitry Kolomenskiy (Post Doc - 2012-2014 Ph.D. Universite de Provence '10) [web]
- Dr. Alexander Bihlo (Post Doc - 2012-2013 Ph.D. Vienna '11) [web] -- Now at Memorial University
- Ivan Gonzalez (Ph.D. 2021) -- (co-supervised with R. Choksi)
- Xi YuanYin (Ph.D. 2021)
- Jack Tisdell (M.Sc. 2021) -- (co-supervised with R. Choksi)
- Geoff McGregor (Ph.D. 2020) [web]
- Ryan Galagusz (Ph.D. Candidate ECE) [web]
- Mathieu Cadiot (M.Sc. 2020) -- (co-supervised with J.-P. Lessard)
- Seth Taylor (M.Sc. 2020) -- (co-supervised with Gantumur Tsogtgerel)
- David Abraham (Ph.D. Candidate ECE) [web]
- Philippe Blain (Master '18) -- (co-supervised with G. Tsogtgerel)
- Xi YuanYin (Master '16) -- (co-supervised with L. Chen)
- Badal Yadav (Master '15) [web]
- Gwenael Peltier (Master '15)
- Dr. Alexandra Tcheng (Ph.D. '15) [web]
- Dr. Lisa Larsson (Ph.D. '14) [web] -- (co-supervised with R. Choksi)
-- - Now at Courant
- Olivier Mercier (Master '13) [web] - Now at Universite de Montreal - CS/OR
- Nelson Feyeux (Master '13) [web]- Now at Universite de Grenoble
- Dr. Alexandre N. Marques (Ph.D. MIT '12) - Now at Embraer
- Yuki Zhang (B.Sc.Math 2020) [web]
- Noah LeFrancois (B.Sc.Physics 2020) [web]
- Florian Seefeld (B.Sc. Honours Math./Phys. 2021) [web]
- Manuel Bolduc (B.Sc. Honours Math./Phys. 2020) [web]
- Shenshun Yao (B.Sc. Honours Math 2019) [web]
- Carl Perreault-Lafleur (B.Sc. Honours Math. 2019) [web]
- Cem Gormezano (B.Sc. Mech.Engr./Math 2018) [web] -- (co-supervised with A. Wan) -- now at Oxford
- Di Zhang (B.Sc. Math. 2019) [web]
- Peter Kaloyannis (CEGEP Marianopolis) [web]
- Jia (Angela) Lu (B.Sc. Math./Bio. 2017) [web]
- Katharine Wells (B.Sc. Math. 2017) [web]
- Fengdi Che (B.Sc. Math. 2018) [web]
- Florestan Brunck (B.Sc. Math./C.S. 2018) [web]
- Zoe Guan (Honors B.S. in Mathematics 2015) - Now Ph.D. student at Harvard
- Zhu Jiaqi (Honors B.S. in Mathematics 2016)
- Raphael Meudec (Master Applied Mathematics - ENSTA - 2016)
- Olivier Melancon (B.S. in Mathematics 2016)
- Fabio Alves (B.S. in Electrical Engineering 2016 - UFMG (Brazil))
- Russell Milne (Honors B.S. in Mathematics 2015)
- Yoel Chetboun (Master Applied Mathematics - ENSTA) (2014)
- Cyrielle Zakini (Master Applied Mathematics - ENSTA) (2014)
- Amine Alaoui Fdili (Master Applied Mathematics - ENSTA) (2014)
- Miles Shang (B.S. in Mathematics '12) - Now at Facebook
- Sebastien Jean (B.S. in Mathematics '12) - Now at Universite de Montreal - CS/OR
- Mareike Adams (B.S. in Mathematics '12) - [web] -- Now at UCSB (Geophysics)
- Genevieve Bourgeois (B.S. in Mathematics '13) - [web] -- Now at Waterloo
- Simon Szatmari (B.S. in Mathematics '13) - [web] -- Now at Leiden University
- Olga Yakovlenko
- Robert Gibson
[This page is best viewed with: Google Chrome, Safari, FireFox version >= 4.0, IE version >= 9.0]
Fluid Dynamics
Droplet Impinging a Soap Film (We=8)
Droplet Impinging a Soap Film (We=18)
Walking Droplet on a Vibrating Fluid Bath (80Hz/4.25g)
DNS of Falling Liquid Film (Transition to 3D regime from a 2D perturbation)
Plume Rising
Bubbles Rising and Merging
Visco-Elastic Fiber Breaking
Visco-Elastic Fiber Stable Equilibrium
2D Euler on Torus (hi-resolution)
Flow Around a Cylinder
Eulerian Elasticity
Elastic Circle Relaxing in a Fluid
Passive Elastic Stick in a Fluid
Active Elastic Rotor in a Fluid
Advection of Curves, Surfaces, and Sets
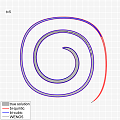
Gradient-Augmented Level Set vs WENO
Characteristic Mapping Method
Characteristic Mapping Method on Open and Closed Curves
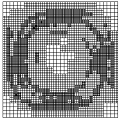
Characteristic Mapping Method on the Mandelbrot Set
Generalized Centroidal Voronoi Tesselation
Generalized CVT of Circles
Generalized CVT of Spheres
Generalized CVT of Rods
Gradient Flows
Coming soon...Traffic Flow
Jamitons: Traffic Jams Non-Linear Waves on a Circle
Jamitons: Traffic Jams Non-Linear Waves on an Infinite Road
Advection Equation
Gradient-Augmented Level Set Method and Jet Schemes
(with B. Seibold and R.R. Rosales)
The level set approach represents surfaces implicitly, and advects
them by evolving a level set function, which is numerically defined on an Eulerian grid.
Here we present an approach that augments the level set function values
by gradient information, and evolves both quantities in a fully coupled fashion.
This maintains the coherence between function values and derivatives, while exploiting
the extra information carried by the derivatives. The method is of comparable quality to
WENO schemes, but with optimally local stencils (performing updates in time by using information
from only a single adjacent grid cell). In addition, structures smaller than the grid size can be
located and tracked, and the extra derivative information can be employed to obtain simple and accurate approximations
to the curvature. We analyze the accuracy and the stability of the new scheme, and perform benchmark tests.
Jet-Schemes are extensions of the GALS Method where higher order derivatives are used to construct the Hermite interpolation. Consequently, higher-order time stepping must used so that the overall (global convergence) order of the scheme is improved. We constructed Jet-Schemes of global order up to 5 in 2D and 3D successfully. The following papers contain details and a comparison of Jet-Schemes with WENO and DG.
[GALSM] [JetScheme1] [JetScheme2]
Jet-Schemes are extensions of the GALS Method where higher order derivatives are used to construct the Hermite interpolation. Consequently, higher-order time stepping must used so that the overall (global convergence) order of the scheme is improved. We constructed Jet-Schemes of global order up to 5 in 2D and 3D successfully. The following papers contain details and a comparison of Jet-Schemes with WENO and DG.
[GALSM] [JetScheme1] [JetScheme2]
Advection of Arbitrary Sets: Characteristic Mapping Method
(with O. Mercier)
In this paper, we present a new numerical method for advecting
arbitrary sets in a vector field. The method computes a transformation
of the domain instead of dealing with particular sets. We propose a way of
decoupling the advection and representation steps of the computations, resulting
in significant reductions in computational times over other methods while still
guaranteeing accuracy. The decoupling also allows one to advect multiple sets at low
computational cost, and makes the method highly parallelizable. Results are presented
in two and three dimensions, and accuracy and efficiency are studied.
[arXiv:1309.2731]
[arXiv:1309.2731]
Adaptive Gradient-Augmented Level Set Method with Multi-Resolution Error Estimation
(with D. Kolomenskyi and K. Schneider)
A space-time adaptive scheme is presented for solving advection equations
in two space dimensions. The gradient-augmented level set method using a semi-Lagrangian
formulation with backward time integration is coupled with a point value multiresolution
analysis using Hermite interpolation. Thus locally refined dyadic spatial grids are introduced
which are efficiently implemented with dynamic quad-tree data structures. For adaptive
time integration, an embedded Runge-Kutta method is employed. The precision of the new
fully adaptive method is analysed and speed up of CPU time and memory compression with
respect to the uniform grid discretization are reported.
[arXiv:1401.7294]
[arXiv:1401.7294]
Poisson Equation with Interface Jump Conditions
Poisson's Equation with Interface Jumps
(with A.N. Marques and R.R. Rosales)
This project has two parts:
(1) Solving Poisson's equation with jump conditions provided on a co-dim 1 interface
(2) Solving piece-wise constant coefficient Poisson's equation with interface provided on a co-dim 1 interface
In the constant coefficient case (1), we developped a technique, the Correction Function Method (CFM) which provides a correction to the RHS of the equation so that the jumps are accurately enforced. This correction is the solution to a local PDE problem (which is fast and easy to solve). Since one may compute the correction to any order of accuracy, and provided the discretization of the Laplacian is of matching order, the method is "in principle" of arbitrary order. We have constructed order 2 and order 4 schemes in 2D successfully. This is detailed in our paper.
The piece-wise constant coefficient case (2) is significantly more complicated. However, we were able to reduce it to the solving 2 CFM problems and one boundary integral (for the potential). This decomposition is close to that of described by Mayo ("The fast solution of Poisson's and the biharmonic equations on irreular regions", SIAM J. NA, 1984). Using the same ideas, we also solve Poisson's equation with arbitrary boundary conditions on an immersed boundary.
We present 2D examples of the algorithm applied to problems involving boundary conditions over complex geometries (with 4th order accuracy), and to a Poisson equation with interfaces across which the solution is discontinuous (with 3rd order accuracy).
[CFM1] [CFM2]
(1) Solving Poisson's equation with jump conditions provided on a co-dim 1 interface
(2) Solving piece-wise constant coefficient Poisson's equation with interface provided on a co-dim 1 interface
In the constant coefficient case (1), we developped a technique, the Correction Function Method (CFM) which provides a correction to the RHS of the equation so that the jumps are accurately enforced. This correction is the solution to a local PDE problem (which is fast and easy to solve). Since one may compute the correction to any order of accuracy, and provided the discretization of the Laplacian is of matching order, the method is "in principle" of arbitrary order. We have constructed order 2 and order 4 schemes in 2D successfully. This is detailed in our paper.
The piece-wise constant coefficient case (2) is significantly more complicated. However, we were able to reduce it to the solving 2 CFM problems and one boundary integral (for the potential). This decomposition is close to that of described by Mayo ("The fast solution of Poisson's and the biharmonic equations on irreular regions", SIAM J. NA, 1984). Using the same ideas, we also solve Poisson's equation with arbitrary boundary conditions on an immersed boundary.
We present 2D examples of the algorithm applied to problems involving boundary conditions over complex geometries (with 4th order accuracy), and to a Poisson equation with interfaces across which the solution is discontinuous (with 3rd order accuracy).
[CFM1] [CFM2]
High-Order Penalization Methods
Sharp-Interface Active Penalty Method
(with D. Shirokoff)
The volume penalty method provides a simple, efficient approach
for solving the incompressible Navier-Stokes equations in domains with
boundaries or in the presence of moving objects. Despite the simplicity,
the method is typically limited to first order spatial accuracy. We demonstrate
that one may achieve high order accuracy by introducing an active penalty term.
One key difference from other works is that we use a sharp, unregularized mask
function. We discuss how to construct the active penalty term, and provide numerical
examples, in dimensions one and two. We demonstrate second and third order
convergence for the heat equation, and second order convergence for the
Navier-Stokes equations. In addition, we show that modifying the penalty
term does not significantly alter the time step restriction from that
of the conventional penalty method.
[arXiv:1303.5681]
[arXiv:1303.5681]
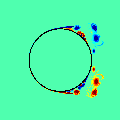
Generalized Voronoi Algorithms
An Iterative Algorithm for Computing the Measure of Generalized Voronoi Regions
(with L. Larsson and R. Choksi)
We present and analyze a fast algorithm for directly computing the measure of
a generalized Voronoi region associated with generators of arbitrary co-dimension. The algorithm
is based upon solving one Eikonal equation to generate a kernel-based operator whose iteration
accumulates \mass" along the closest generator. In particular, the algorithm does not require the
computation of the ridge set (Voronoi diagram) nor the gradient of the solution to the Eikonal
equation. The algorithm is shown to be .rst order and converge very quickly. Several illustrations
are presented including the computation of measures of in
uence associated with the Los Angeles
County highway system. The method can also be used for the fast computation of the centroid and
higher moments of the generalized Voronoi regions.
Gradient Flows
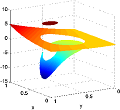
Global Analysis for Minimizers of Non-Convex Functionals: A Simple Approach via Convex Approximation
(with D. Shirokoff and R. Choksi)
We consider mass-constrained minimizers for a class of non-convex energy functionals
involving double-well potentials. Based upon a global convex lower bound to the energy, we introduce
a simple strategy to .nd su.cient conditions to infer whether a given critical point is a global
minimizer. We show that this strategy works well for the simplest of critical points, the constant
state. In doing so, we derive an almost optimal lower bound on the order-disorder curve for the
Ohta-Kawasaki energy. Focusing on the lamellar phase, we discuss how this strategy extends to
non-constant critical points.
[PDF]
[PDF]
Invariant Numerical Methods and Lie Groups
Invariant Discretization Schemes Using Evolution-Projection Techniques
(with A. Bihlo)
Finite difference discretization schemes preserving a subgroup of the maximal Lie invariance group of the one-dimensional linear heat equation are determined. These invariant schemes are constructed using the invariantization procedure for non-invariant schemes of the heat equation in computational coordinates. We propose a new methodology for handling moving discretization grids which are generally indispensable for invariant numerical schemes. The idea is to use the invariant grid equation, which determines the locations of the grid point at the next time level only for a single integration step and then to project the obtained solution to the regular grid using invariant interpolation schemes. This guarantees that the scheme is invariant and allows one to work on the simpler stationary grids. The discretization errors of the invariant schemes are established and their convergence rates are estimated. Numerical tests are carried out to shed some light on the numerical properties of invariant discretization schemes using the proposed evolution-projection strategy.
[PDF]
[PDF]
Convecting Reference Frames and Invariant Numerical Models
(with A. Bihlo)
In the recent paper by Bernardini et al. [J. Comput. Phys. 232 (2013), 1-6] the discrepancy in the performance of finite difference and spectral models for simulations of flows with a preferential direction of propagation was studied. In a simplified investigation carried out using the viscous Burgers equation the authors attributed the poorer numerical results of finite difference models to a violation of Galilean invariance in the discretization and propose to carry out the computations in a reference frame moving with the bulk velocity of the flow. Here we further discuss this problem and relate it to known results on invariant discretization schemes. Non-invariant and invariant finite difference discretizations of Burgers equation are proposed and compared with the discretization using the remedy proposed by Bernardini et al.
[ArXiv:1301.5955]
[ArXiv:1301.5955]
Multi-phase Flows
By leveraging the Subgrid accuracy of the methods presented above, we can simulate the dynamics of a droplet of water impinging on a soap film.
These simulations were performed on a regular Cartesian grid and capture quantatively the various regimes found in the experiments of T. Gilet and J. Bush [Their Paper].
Using a similar approach, our method can simulate the problem of partial coalescence. The subgrid accuracy of the method allows here too to compare quantatively with experiments.
These simulations were performed on a regular Cartesian grid and capture quantatively the various regimes found in the experiments of T. Gilet and J. Bush [Their Paper].
Using a similar approach, our method can simulate the problem of partial coalescence. The subgrid accuracy of the method allows here too to compare quantatively with experiments.
Falling Liquid Films
(with X.D. Liu and S. Banerjee)
Liquid films are important in many industrial applications, but also from a
fundamental point of view, they are important two-phase flow systems. In this
paper, we develop a sharp interface/level set method for the Direct Numerical
Simulation (DNS) of liquid films with large interfacial deformations, and large
density ratio between the liquid and the gas phase. We use the ghost fluid
method to capture the interface motion without smoothing properties across it,
and adopt a maximization scheme for the implicit treatment of the viscous
term in the Navier–Stokes equations. Because liquid films have very low
average depth compared to the distance between waves, several innovations are
required to handle solving the equations on grid structures of high aspect ratio.
Two-dimensional (2D) calculations for wavy films falling down a vertical wall
are presented, and good agreement is found when numerical solutions are
directly compared with the experiments of Nosoko et al. [1]. Some results are
also presented for falling liquid films transitioning naturally from 2D to 3D
surface wave structures demonstrating the potential of the method for 3D fully
coupled two-phase liquid films simulations.
[PDF]
[PDF]
Magma Flow
(with J. Suckale, B. Hager, L.T. Elkins-Tanton)
Concentric Fluid Shells Satability and Fiber Drawing
(with X. Liang, D. S. Deng, Y. Fink, S. G. Johnson)
Motivated by complex multi-fluid geometries currently being explored in fibre-device
manufacturing, we study capillary instabilities in concentric cylindrical flows of N
fluids with arbitrary viscosities, thicknesses, densities, and surface tensions in both the
Stokes regime and for the full Navier–Stokes problem. Generalizing previous work by
Tomotika (N=2), Stone and Brenner (N=3, equal viscosities) and others, we present
a full linear stability analysis of the growth modes and rates, reducing the system to
a linear generalized eigenproblem in the Stokes case. Furthermore, we demonstrate
by Plateau-style geometrical arguments that only axisymmetric instabilities need be
considered. We show that the N=3 case is already sufficient to obtain several
interesting phenomena: limiting cases of thin shells or low shell viscosity that
reduce to N=2 problems, and a system with competing breakup processes at very
different length scales. The latter is demonstrated with full three-dimensional Stokesflow
simulations. Many N > 3 cases remain to be explored, and as a first step we
discuss two illustrative N->infinity cases, an alternating-layer structure and a geometry
with a continuously varying viscosity.
[ShellStability] [FiberDrawing]
[ShellStability] [FiberDrawing]
Concentrated Solar Power on Demand (CSPonD)
(with A. H. Slocum, D. S. Codd , J. Buongiorno, C. Forsberg, T. McKrell, C. N. Papanicolas, A. Ghobeity, C. J. Noone, S. Passerini, F. Rojas, A. Mitsos)
Traffic Flow
Self-Sustained Nonlinear Waves in Traffic Flow
(with M. Flynn, A. Kasimov, B. Seibold, and R.R. Rosales)
Our research is based on the observation that the considered traffic models are similar to the equations that describe detonation waves produced by explosions. Employing the theory of denotation waves, we have developed ways to analytically predict the exact shape and the speed of propagation of jamitons. Numerical simulations of the considered traffic models show that the predicted jamiton solutions are in fact achieved, if the initial traffic density is sufficiently dense. The considered jamitons can qualitatively be found both in observed real traffic as well as in experiments. The theoretical description of the jamiton solution admits a better understanding of their behavior.
[TrafficFlow] [Jamitons-ArXiv:0809.2828]
We maintain a web page at MIT regarding this project: [MIT Traffic Flow Page].
[TrafficFlow] [Jamitons-ArXiv:0809.2828]
We maintain a web page at MIT regarding this project: [MIT Traffic Flow Page].
Under Review
- S Xu, M Mei, JC Nave, W Sheng. (2024). Viscous shock waves of Burgers equation with fast diffusion and singularity
[ArXiv:2404.10941] - J Bergmann, T Maurel-Oujia, JC Nave, K Schneider. (2024). Singularity formation of vortex sheets in 2D Euler equations using the characteristic mapping method
[ArXiv:2404.02008] - X Li, J Li, M Mei, JC Nave. (2024). Nonlinear stability of shock profiles to Burgers' equation with critical fast diffusion and singularity
[ArXiv:2402.09630] - M. Cadiot, J.-P. Lessard, J.-C. Nave. (2024). Stationary non-radial localized patterns in the planar Swift-Hohenberg PDE: constructive proofs of existence
[ArXiv:2403.10450] - D. Tageddine, J.-C. Nave. (2023). Statistical Fluctuation of Infinitesimal Spaces
[ArXiv:2304.10617] - S Taylor, JC Nave. (2023). A characteristic mapping method for incompressible hydrodynamics on a rotating sphere
[ArXiv:2302.01205] - D Tageddine, JC Nave. (2022). Noncommutative Differential Geometry on Infinitesimal Spaces
[ArXiv:2209.12929] - G. McGregor and J.-C. Nave. Parametric Interpolation Framework for 1-D Scalar Conservation Laws with Non-Convex Flux Functions
[ArXiv:1911.13174]
Publications
2024:
- M Cadiot, JP Lessard, JC Nave. (2023). Rigorous computation of solutions of semi-linear PDEs on unbounded domains via spectral methods
[ArXiv:2302.12877] - P Krah, XY Yin, J Bergmann, JC Nave, K Schneider. (2023). A characteristic mapping method for Vlasov-Poisson with extreme resolution properties
[ArXiv:2311.09379] - I Gonzalez, J Tisdell, R Choksi, JC Nave. (2023). Emergence of diverse collective behaviors from local topological perception
[ArXiv:2111.03448]
2023:
- XY Yin, K Schneider, JC Nave. (2023). A Characteristic Mapping Method for the three-dimensional incompressible Euler equations. (2023) Journal of Computational Physics. 477
[PDF]
[ArXiv:2107.03504] - Seth Taylor, Jean-Christophe Nave. A projection-based Characteristic Mapping method for tracer transport on the sphere. (2023) Journal of Computational Physics. 477
[PDF]
[ArXiv:2106.13170]
2022:
- Y.-M. Law, and J.-C. Nave. High-Order FDTD Schemes for Maxwell's Interface Problems with Discontinuous Coefficients and Complex Interfaces Based on the Correction Function Method, (2022) J. Sci. Comp. 91
[PDF]
[ArXiv:2101.05417] - G. McGregor and J.-C. Nave. Parametric Interpolation Framework for Scalar Conservation Laws. (2022) J. Comp. Applied Math.
[PDF]
[ArXiv:1910.13486] - ATS Wan, A. Bihlo, J.-C. Nave. Conservative integrators for many-body problems. (2022) Journal of Computational Physics. 466
[PDF]
[ArXiv:2106.06641] - C. Gormezano, J.-C. Nave, ATS Wan. Conservative Integrators for Vortex Blob Methods on the Plane, (2022) Journal of Computational Physics. 469
[PDF]
[ArXiv:2111.01233]
2021:
- Y.-M. Law, and J.-C. Nave. FDTD schemes for Maxwell interface problems with perfect electric conductors based on the correction function method, (2021) J. Sci. Comp. 88:72
[PDF]
[ArXiv:1909.10570] - X.-Y. Yin, L. Chen, J.-C. Nave. A diffusion-driven Characteristic Mapping method for particle management, (2021) SIAM J. Sci. Comp. (SISC) 43(5)
[PDF]
[ArXiv:2008.13076] - X.-Y. Yin, O. Mercier, B.Yadav, K. Schneider, J.-C Nave. A Characteristic Mapping Method for the two-dimensional incompressible Euler equations. (2021) J. Comp. Phys. 424
[PDF]
[ArXiv:1910.10841] - Isha Shukla, Fan Wang, Saviz Mowlavi, Amy Guyomard, Xiangdong Liang, Steven G Johnson, J-C Nave. Reduced model for capillary breakup with thermal gradients: Predictions and computational validation, (2021) Physics of Fluids. 33(12)
[PDF]
[ArXiv:2104.11671] - I Gonzalez, R Choksi, J.-C. Nave. A simple geometric method for navigating the energy landscape of centroidal Voronoi tessellations, (2021) SIAM J. Sci. Comp. (SISC) 43(2)
[PDF]
[ArXiv:2005.00094]
2020:
- A Navarra, R Wilson, R Parra, N Toro, A Ross, JC Nave, PJ Mackey. Quantitative methods to support data acquisition modernization within copper smelters. (2020) Processes. 8(11)
[PDF] - Y.-M. Law, A. N. Marques and J.-C. Nave. High-order finite difference scheme for Maxwell's equation with interface jump conditions for complex interfaces, (2020) J. Sci. Comp. 82:56
[PDF]
[ArXiv:1810.00448] - O. Mercier, X.-Y. Yin, J.-C. Nave. The characteristic mapping method for the linear advection of arbitrary sets. (2020) SIAM J. Sci. Comp. (SISC) 43(3)
[ArXiv:1309.2731]
2019:
- A. N. Marques, J.-C. Nave, and R. R. Rosales. Imposing jump conditions on nonconforming interfaces via least squares minimization. (2019) J. Comp. Phys. Volume 397, 108869
[PDF]
[ArXiv:1710.11016] - G. McGregor and J.-C. Nave. Area-preserving geometric Hermite interpolation. (2019) J. Comp. and Applied Math. 361, 236-248
[PDF]
[ArXiv:1810.01285]
2018:
- A. Wan and J.-C. Nave. On the arbitrarily long-term stability of conservative methods, (2018) SIAM J. Numer. Anal. 56 (5), 2751-2775
[ArXiv:1607.06160] - D. Abraham, J.-C. Nave, A. N. Marques. A Correction Function Method for the Wave Equation with Interface Jump Conditions. (2018) J. Comp. Phys. Volume 353, Pages 281-299.
[ArXiv:1609.05379]
2017:
- A. Wan, A. Bihlo, and J-C. Nave. Conservative methods for dynamical systems, (2017) SIAM J. Numer. Anal. 55 (5), 2255-2285
[ArXiv:1612.02417] - A. N. Marques, J.-C. Nave, and R. R. Rosales. High order solution of Poisson problems with piecewise constant coefficients and interface jumps. (2017) J. Comp. Phys. Volume 335, Pages 497-515
[ArXiv:1401.8084]
2016:
- A. Tcheng and J.-C. Nave. A Fast-Marching algorithm for non-monotonically evolving fronts. (2016) SIAM J. Sci. Comput., 38(4), A2307-A2333
[PDF] - A. Tcheng and J.-C. Nave. A low complexity algorithm for non-monotonically evolving fronts. J. Sci. Comput. (2016).
[PDF] - L. Larsson, R. Choksi, and J.C. Nave. Geometric Self-assembly of Rigid Shapes: A Simple Voronoi Approach. (2016) SIAM J. Appl. Math., 76(3), 1101-1125
[PDF] - Kolomenskiy D, Maeda M, Engels T, Liu H, Schneider K, Nave J-C (2016) Aerodynamic Ground Effect in Fruitfly Sized Insect Takeoff. PLoS ONE 11(3)
[PDF]
2015:
- Ryan Galagusz, David Shirokoff and Jean-Christophe Nave. A Fourier penalty method for solving the time dependent Maxwell's equations in domains with curved boundaries. (Accepted)
[ArXiv:1503.03914] - A. Wan, A. Bihlo, and J-C. Nave. The multiplier method to construct conservative finite-difference schemes for ordinary and partial differential equations. (Accepted)
[ArXiv:1411.7720] - Dmitry Kolomenskiy, J.-C. Nave, and K. Schneider. Adaptive gradient-augmented level set method with multiresolution error estimation. (Accepted)
[ArXiv:1401.7294] - D. Shirokoff, R. Choksi, and J-C. Nave. Global analysis for minimizers of non-convex functionals: A simple approach via convex approximation. (Accepted)
[PDF]
2014:
- A. Bihlo and J.-C. Nave. Convecting reference frames and invariant numerical models. J. Comp. Phys., 271:656-663 (2014)
[ArXiv:1301.5955] - D. Shirokoff and J.-C. Nave. A high-order penalization method for fluid flows with irregular boundaries. J. Sci. Comp., (April):1-25 (2014)
[ArXiv:1303.5681] - L. Larson, R. Choksi, and J.-C. Nave. An iterative algorithm for computing measures of generalized voronoi regions. SIAM J. Sci. Comp., 36(2):792-827 (2014)
[PDF]
2013:
- A. Bihlo and J.-C. Nave. Invariant discretization schemes using evolution projection techniques. SIGMA, 9, (2013)
[PDF] - H. Kohno and J.-C. Nave. A mesh-less method for the advection equation and its gradient. Computer Physics Communications., (2013)
[PDF]
2012:
- P. Chidyagwal, J.-C. Nave, R.R. Rosales, and B. Seibold. A comparative study of the efficiency of jet schemes. Int. J. Num. Anal. Model. - B, (2012)
[PDF] - B. Seibold, R.R. Rosales, and J.-C. Nave. Jet schemes for advection problems. Discr. and Cont. Dynam. Syst. - B, (2012)
[PDF] - K. Kamrin, C. H. Rycroft, and J.-C. Nave. Reference map technique for finite-strain elasticity and fluid-solid interaction. J. Mech. and Phys. Solids, (2012)
[PDF]
2011:
- J. Suckale, B. Hager, L.T. Elkins-Tanton, J.-C. Nave, Reply to the comment by Mike R. James et al. on It takes three to tango: 2. Bubble dynamics in basaltic volcanoes and ramifications for modeling normal Strombolian activity. Journal of Geophysical Research, 116, B06208 (2011)
[PDF] - A. H. Slocum, D. S. Codd , J. Buongiorno, C. Forsberg, T. McKrell, J.-C. Nave, C. N. Papanicolas, A. Ghobeity, C. J. Noone, S. Passerini, F. Rojas, A. Mitsos, Concentrated solar power on demand, Solar Energy 85 (2011) 1519-1529.
[PDF] - X. Liang, D. S. Deng, J.-C. Nave, S. G. Johnson, Linear stability analysis of capillary instabilities for concentric cylindrical shells, J. Fluid Mech., 260, (2011)
[PDF] - D. S. Deng, J.-C. Nave, X. Liang, S. G. Johnson, Y. Fink, Exploration of in-fiber nanostructures from capillary instability, Optics Express , Vol. 19, No. 17, (2011).
[PDF] - A. N. Marques, J.-C. Nave, R. R. Rosales, A Correction Function Method for Poisson problems with interface jump conditions, Journal of Computational Physics 230 (2011)
[PDF]
2010:
- J.-C. Nave, S. Banerjee, X.D. Liu, "Direct Numerical Simulation of Liquid Films with Large Interfacial Deformation", Studies in Applied Mathematics, (2010) 125, 153-77
[PDF] - J. Suckale, J.-C. Nave, B. Hager, L.T. Elkins-Tanton, "Simulations of buoyancy-driven flow in the presence of large viscosity contrasts: I. Numerical approach", J. Geophys. Rev., (2010) 115, B07409, 16 pp
[PDF] - J. Suckale, B. Hager, L.T. Elkins-Tanton, J.-C. Nave, "Simulations of buoyancy-driven flow in the presence of large viscosity contrasts: II. Implications for modeling normal Strombolian-type activity", J. Geophys. Rev. (2010) 115, B07410, 17 pp.
[PDF] - J.-C. Nave, R.R. Rosales, B. Seibold, "A Gradient-Augmented Level Set Method with an Optimally Local, Coherent Advection Scheme", J. Comp. Phys., (2010) 229, 3802-27.
[PDF]
Older Papers:
- J. Crest, J.-C. Nave, S. Pabba, R. W. Cohn, and G.H. McKinley. Formation of nanofibers by capillary-driven thinning of drying visco-elastic filaments.
[PDF] - M.R. Flynn, A.R. Kasimov, J.-C. Nave, R.R. Rosales, B. Seibold, "Self-Sustained Nonlinear Waves in Traffic Flow", Phys.Rev.E 79, 056113 (2009)
[PDF] - S. Banerjee, V. Badalassi, V. Dwivedi, J.-C. Nave, D. Hall, "The Direct Numerical Simulation of Two-Phase Flows with Interface Capturing Methods", La Houille Blanche (2005)
[PDF] - K.N. Premnath, J.-C. Nave, S. Banerjee, "Computation of multiphase flows with lattice boltzman methods", Invited Paper ASME, IMECE (2005)
[.] - S. Smolentsev, N. B. Morley, B. Freeze, R. Miraghaie, J.-C. Nave, S. Banerjee, A. Ying, M. Abdou, "Thermofluid Modeling and Experiments for Free Surface Flows of Low-Conductivity Fluid in Fusion Systems", Fusion Engineering and Design (2004).
[LINK] - J.-C. Nave, S. Banerjee, "Direct Numerical Simulation of Wavy Falling Liquid Films", 5th International Conference on Multiphase Flow, ICMF (2004)
[.]
Notes:
- M.R. Flynn, A.R. Kasimov, J.-C. Nave, R.R. Rosales, B. Seibold, "On "jamitons", Self-Sustained Nonlinear Traffic Waves", available arXiv:0809.2828, (2008)
[[ArXiv:0809.2828]] - M. Shang, J.-C. Nave, A Probabilistic Method for Topological Control in Cloth Simulations (2012)
[PDF]

Contact
Department of Mathematics and Statistics
McGill University
Burnside Hall, Room 1121
805 Sherbrooke West
Montreal, QC, H3A 0B9
Canada
jcnave@math.mcgill.ca
Phone: (514) 398-3048
Fax: (514)-398-3899
Positions Available
@ Ph.D. level:- You MUST have a degree in Math.
- You should read some of my papers before contacting me.
- I will not reply to generic emails.
@ Postdoc level:
- Several openings are available through the CRM-ISM Postdoctoral Fellowships program.