[Warning: the
level of precision is set to a beginning graduate student level. The experts
will find here some inaccurate, though morally true, passages.]
I am currently working in the field of arithmetic geometry, which studies algebraic geometry in settings arising from number theory. Some of the key words in this field are abelian varieties, moduli spaces, modular forms.
Abelian varieties
are higher dimensional analogs of elliptic curves. An elliptic curves is
a complete non-singular curve of genus 1 (with a given point). Such a curve
is a commutative algebraic group, i.e. there are ways to add and subtract
points on the curve to get other points and these laws are such that one
gets a group; moreover, these addition and subtraction laws are defined
by polynomial equations. The simplest way to give an elliptic curve (over
a field of characteristic different from 2) is by giving an equation of
the form E: y2 = 4x3 + ax + b, such that the
polynomial 4x3 + ax + b has distinct roots. The elliptic
curve consists of the solutions to this equation together with an extra
point "at infinity" that serves as the zero point.
Over the complex numbers
such a curve E is a compact oriented surface of genus 1 and is isomorphic
as a Riemann surface to C/L, where L is a lattice
in the complex numbers C. The exact function from C/L
to E has the form z -> (P'(z), P(z)) where P
is Weierstrass' P-function, for which a complete expression as a
power series is available. One can show that two elliptic curves over the
complex numbers are isomorphic if and only if the corresponding lattices
are homothetic. 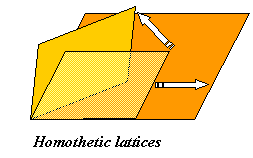 Thus,
the set of isomorphism classes of elliptic curves over the complex numbers
is in bijection with homothety classes of lattices. The latter can be shown
to be in a natural bijection with A1(C) := SL(2,Z)\H,
where H is the complex upper half plane on which the group SL(2,
Z)
acts by Mobius transformations. It is the (coarse) moduli space
of elliptic curves. Modular forms can be defined as sections of line bundles
over A1(C).
Thus,
the set of isomorphism classes of elliptic curves over the complex numbers
is in bijection with homothety classes of lattices. The latter can be shown
to be in a natural bijection with A1(C) := SL(2,Z)\H,
where H is the complex upper half plane on which the group SL(2,
Z)
acts by Mobius transformations. It is the (coarse) moduli space
of elliptic curves. Modular forms can be defined as sections of line bundles
over A1(C).
Abelian varieties are commutative complete connected algebraic groups. In general it is very difficult to give explicit equations for abelian varieties. Over the complex numbers, abelian varieties of dimension g are g-dimensional tori, i.e. isomorphic as complex analytic manifolds to Cg/L where L is a lattice in the g-dimensional complex vector space Cg. However, the lattice L must be such that the quotient Cg/L carries "lots" of meromorphic functions, because the field of meromorphic functions on a complex g-dimensional algebraic variety is of transcendence degree g. This puts some severe restrictions on L, called Riemann's bilinear relations. Nonetheless, in essence the story is the same: again two abelian varieties are isomorphic if and only if the corresponding lattices are homothetic; the space Hg of the lattices arising from (principally polarized) abelian varieties has a natural structure of a complex manifold and the equivalence relation between lattices amounts to taking a quotient of Hg by Sp(2g,Z) - the integral symplectic 2gx2g matrices. The quotient space Ag(C) := SP(2g,Z)\Hg is the (coarse) moduli space for complex g-dimensional (principally polarized) abelian varieties. Siegel modular forms are sections of certain line bundles over Ag(C).
Much of my own research has to do with the analogous objects and constructions in characteristic p, or over p-adic numbers. One defines abelian varieties over any commutative ring R as (essentially) projective connected commutative algebraic groups and shows that there is a moduli space Ag(R) for abelian varieties. One can define line bundles on Ag(R) such that modular forms are defined as sections of these line bundles.
The geometry of these
moduli spaces and properties of modular forms are one of the focal points
of arithmetic geometry (and my own research). Hard questions in number
theory, as the source of representations for the absolute Galois group
Gal(Qalg/Q), Fermat's last theorem, values of
L-functions,
are intimately related to (and are often solved or at least studied by)
these moduli spaces and modular forms. The particular questions I am studying
are the geometry of these moduli spaces: various stratifications and their
intersections, Chow rings and intersection theory, congruences between
modular forms and applications to Galois representations and special values
of L-functions, and intersections with the Torelli locus (the moduli
space of curves of genus g). These research subjects are undergoing
intense development for many years. There are many possible projects, both
of computational and of theoretical nature, at the level of Masters, Ph.D.
and Post-doctoral level.

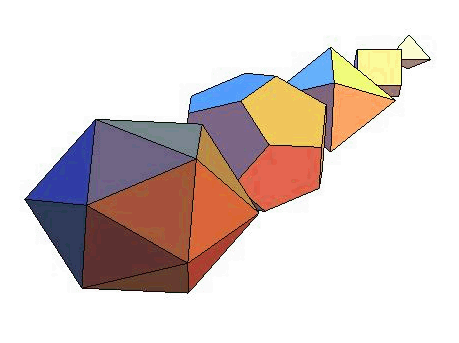
[For those who
know more: I am studying the Newton, Ekedahl-Oort and Type stratifications
on Hilbert modular varieties. The diagram on the right gives (in the example
of g=8) the hierarchy of the strata Andreatta and I defined for
Hilbert modular varieties modulo a maximally ramified prime. A strata
corresponds to a pair (i,j) and its boundary are the strata that
are "above and connected to it" in the diagram; I am studying tautological
classes in the setting of Shimura varieties of PEL type and moduli spaces
of curves; I am studying p-adic Hilbert modular forms and congruences
arising from applications of the theory to Eisenstein series; I am studying
deformation theory of abelian varieties and p-divisible groups with
special interests in displays and local models. Many of the projects above
are joint; my collaborators and coauthors are: F. Andreatta (Padova), E.
Bachmat (Beer-Sheva), E. DeShalit (Hebrew U.), B. Moonen (Amsterdam), F.
Oort (Utrecht) and R. Pries (Columbia U.). ]
I also have a long standing interest in applications of moduli spaces and modular forms for problems in class field theory (which were one of the original motivations for the theory) and wrote my Ph.D. thesis was about such problems. The main idea is to use special values of modular forms + information on the moduli space to derive properties of these special values. The key words here are class field theory, complex multiplication, units. I can offer here a very interesting Masters project of a computational nature, involving deep mathematics.
[For those who know
more: In
my thesis, and in a joint work with de Shalit, there are constructions
of invariants in ray class fields of CM fields, arising from evaluation
of Siegel modular forms at CM points. The moduli interpretation, arithmetic
intersection theory and Shimura reciprocity law are used to get information
on these invariants. There is no numerical information. Such information
would be of great interest.]